Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-23T10:08:13.545Z Has data issue: false hasContentIssue false
  • English
  • Français

DISMANTLABLE CLASSIFYING SPACE FOR THE FAMILY OF PARABOLIC SUBGROUPS OF A RELATIVELY HYPERBOLIC GROUP

Part of: Fiber spaces and bundles Special aspects of infinite or finite groups

Published online by Cambridge University Press:  11 April 2017

Eduardo Martínez-Pedroza  and
Piotr Przytycki
Eduardo Martínez-Pedroza
Affiliation:
Memorial University, St. John’s, Newfoundland, Canada A1C 5S7 ([email protected])
Piotr Przytycki
Affiliation:
McGill University, Montreal, Quebec, Canada H3A 0B9 ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 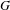$G$ be a group hyperbolic relative to a finite collection of subgroups 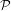${\mathcal{P}}$. Let 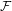${\mathcal{F}}$ be the family of subgroups consisting of all the conjugates of subgroups in 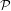${\mathcal{P}}$, all their subgroups, and all finite subgroups. Then there is a cocompact model for 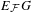$E_{{\mathcal{F}}}G$. This result was known in the torsion-free case. In the presence of torsion, a new approach was necessary. Our method is to exploit the notion of dismantlability. A number of sample applications are discussed.

Keywords

20-XX group theory and generalizations57-XX manifolds and cell complexes55-XX algebraic topology

MSC classification

Primary: 20F67: Hyperbolic groups and nonpositively curved groups 55R35: Classifying spaces of groups and $H$-spaces 57S30: Discontinuous groups of transformations
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 18 , Issue 2 , March 2019 , pp. 329 - 345
Copyright
© Cambridge University Press 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alonso, J. M., Brady, T., Cooper, D., Ferlini, V., Lustig, M., Mihalik, M., Shapiro, M. and Short, H., Notes on word hyperbolic groups, in Group Theory from a Geometrical Viewpoint (Trieste, 1990), pp. 3–63 (World Scientific Publishing, River Edge, NJ, 1991). Edited by Short.Google Scholar
Barmak, J. A. and Minian, E. G., Strong homotopy types, nerves and collapses, Discrete Comput. Geom. 47(2) (2012), 301–328.Google Scholar
Bowditch, B. H., Relatively hyperbolic groups, Int. J. Algebra Comput. 22(3) (2012), 1250016–1250066.Google Scholar
Bredon, G. E., Equivariant Cohomology Theories, Lecture Notes in Mathematics, volume 34 (Springer, Berlin–New York, 1967).Google Scholar
Bridson, M. R. and Haefliger, A., Metric Spaces of Non-positive Curvature, Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], volume 319, (Springer, Berlin, 1999).Google Scholar
Chepoi, V. and Osajda, D., Dismantlability of weakly systolic complexes and applications, Trans. Amer. Math. Soc. 367(2) (2015), 1247–1272.Google Scholar
Dahmani, F., Les groupes relativement hyperboliques et leurs bords, PhD thesis (2003).Google Scholar
Dahmani, F., Classifying spaces and boundaries for relatively hyperbolic groups, Proc. Lond. Math. Soc. (3) 86(3) (2003), 666–684.Google Scholar
Druţu, C. and Sapir, M. V., Groups acting on tree-graded spaces and splittings of relatively hyperbolic groups, Adv. Math. 217(3) (2008), 1313–1367.Google Scholar
Fletcher, J. L., Homological Group Invariants, PhD thesis (1998).Google Scholar
Gersten, S. M., Subgroups of word hyperbolic groups in dimension 2, J. Lond. Math. Soc. (2) 54(2) (1996), 261–283.Google Scholar
Hanlon, R. G. and Martínez-Pedroza, E., A subgroup theorem for homological filling functions, Groups Geom. Dyn. 10(3) (2016), 867–883.Google Scholar
Hensel, S., Osajda, D. and Przytycki, P., Realisation and dismantlability, Geom. Topol. 18(4) (2014), 2079–2126.Google Scholar
Hruska, G. C., Relative hyperbolicity and relative quasiconvexity for countable groups, Algebr. Geom. Topol. 10(3) (2010), 1807–1856.Google Scholar
Lang, U., Injective hulls of certain discrete metric spaces and groups, J. Topol. Anal. 5(3) (2013), 297–331.Google Scholar
Lück, W., Transformation Groups and Algebraic K-theory, Lecture Notes in Mathematics, volume 1408 (Springer, Berlin, 1989). Mathematica Gottingensis.Google Scholar
Lück, W. and Meintrup, D., On the universal space for group actions with compact isotropy, in Geometry and Topology: Aarhus (1998), Contemporary Mathematics, volume 258, pp. 293–305 (American Mathematical Society, Providence, RI, 2000).Google Scholar
Martínez-Pedroza, E., Subgroups of relatively hyperbolic groups of Bredon cohomological dimension 2, preprint, 2015, arXiv:1508.04865.Google Scholar
Martínez-Pedroza, E., A note on fine graphs and homological isoperimetric inequalities, Canad. Math. Bull. 59(1) (2016), 170–181.Google Scholar
Martínez-Pedroza, E. and Wise, D. T., Relative quasiconvexity using fine hyperbolic graphs, Algebr. Geom. Topol. 11(1) (2011), 477–501.Google Scholar
Meintrup, D. and Schick, T., A model for the universal space for proper actions of a hyperbolic group, New York J. Math. 8(1–7) (2002), (electronic).Google Scholar
Mineyev, I. and Yaman, A., Relative hyperbolicity and bounded cohomology, Available at http://www.math.uiuc.edu/ mineyev/math/art/rel-hyp.pdf, 2007.Google Scholar
Osin, D. V., Relatively hyperbolic groups: intrinsic geometry, algebraic properties, and algorithmic problems, Mem. Amer. Math. Soc. 179(843) (2006), vi+100.Google Scholar
Osin, D. V., Peripheral fillings of relatively hyperbolic groups, Invent. Math. 167(2) (2007), 295–326.Google Scholar
Polat, N., Finite invariant simplices in infinite graphs, Period. Math. Hungar. 27(2) (1993), 125–136.Google Scholar
Segev, Y., Some remarks on finite 1-acyclic and collapsible complexes, J. Combin. Theory Ser. A 65(1) (1994), 137–150.Google Scholar
tom Dieck, T., Transformation Groups, de Gruyter Studies in Mathematics, volume 8 (Walter de Gruyter & Co., Berlin, 1987).Google Scholar