Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-23T12:38:03.380Z Has data issue: false hasContentIssue false
  • English
  • Français

COHERENCE, LOCAL INDICABILITY AND NONPOSITIVE IMMERSIONS

Part of: Special aspects of infinite or finite groups Low-dimensional topology

Published online by Cambridge University Press:  17 September 2020

Daniel T. Wise Open the ORCID record for Daniel T. Wise [Opens in a new window]
Daniel T. Wise*
Affiliation:
Dept. of Math. & Stats., McGill University, Montreal, QuebecH3A 2K6, Canada ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We examine 2-complexes 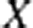$X$ with the property that for any compact connected 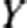$Y$, and immersion $Y\rightarrow X$, either 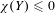$\unicode[STIX]{x1D712}(Y)\leqslant 0$ or 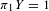$\unicode[STIX]{x1D70B}_{1}Y=1$. The mapping torus of an endomorphism of a free group has this property. Every irreducible 3-manifold with boundary has a spine with this property. We show that the fundamental group of any 2-complex with this property is locally indicable. We outline evidence supporting the conjecture that this property implies coherence. We connect the property to asphericity. Finally, we prove coherence for 2-complexes with a stricter form of this property. As a corollary, every one-relator group with torsion is coherent.

Keywords

coherent groupslocally indicable groups

MSC classification

Primary: 20F05: Generators, relations, and presentations 57M20: Two-dimensional complexes
Secondary: 20F67: Hyperbolic groups and nonpositively curved groups 57M07: Topological methods in group theory
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 21 , Issue 2 , March 2022 , pp. 659 - 674
Check for updates
Copyright
© The Author(s) 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Research supported by NSERC.

References

Corson, J. M. and Trace, B., Diagrammatically reducible complexes and Haken manifolds, J. Austral. Math. Soc. Ser. A 69(1) (2000), 116–126.Google Scholar
Feighn, M. and Handel, M., Mapping tori of free group automorphisms are coherent, Ann. of Math. (2) 149(3) (1999), 1061–1077.10.2307/121081CrossRefGoogle Scholar
Gaster, J. and Wise, D. T., Bicollapsibility and groups with torsion, Preprint, 2018, arXiv:1810.12377.Google Scholar
Gersten, S. M., Reducible diagrams and equations over groups, in Essays in Group Theory, pp. 15–73 (Springer, New York, Berlin, 1987).10.1007/978-1-4613-9586-7_2CrossRefGoogle Scholar
Helfer, J. and Wise, D. T., Counting cycles in labeled graphs: the nonpositive immersion property for one-relator groups, Int. Math. Res. Not. IMRN (9) 9 (2016), 2813–2827.10.1093/imrn/rnv208CrossRefGoogle Scholar
Howie, J., On pairs of 2-complexes and systems of equations over groups, J. Reine Angew. Math. 324 (1981), 165–174.Google Scholar
Howie, J., On locally indicable groups, Math. Z. 180(4) (1982), 445–461.10.1007/BF01214717CrossRefGoogle Scholar
Howie, J., How to generalize one-relator group theory, in Combinatorial Group Theory and Topology, (ed. Gersten, S. M. and Stallings, J. R.), pp. 53–78 (Princeton University Press, Princeton, NJ, 1987).CrossRefGoogle Scholar
Hruska, G. C. and Wise, D. T., Towers, ladders and the B. B. Newman spelling theorem, J. Aust. Math. Soc. 71(1) (2001), 53–69.10.1017/S1446788700002718CrossRefGoogle Scholar
Huebschmann, J., Aspherical 2-complexes and an unsettled problem of J. H. C. Whitehead, Math. Ann. 258(1) (1981/82), 17–37.CrossRefGoogle Scholar
Louder, L. and Wilton, H., Stackings and the W-cycles conjecture, Canad. Math. Bull. 60(3) (2017), 604–612.CrossRefGoogle Scholar
Lyndon, R. C. and Schupp, P. E., Combinatorial Group Theory, Ergebnisse der Mathematik und ihrer Grenzgebiete, Band 89 (Springer, Berlin, 1977).Google Scholar
Martínez-Pedroza, E. and Wise, D. T., Coherence and negative sectional curvature in complexes of groups, Michigan Math. J. 62(3) (2013), 507–536.Google Scholar
McCammond, J. P. and Wise, D. T., Fans and ladders in small cancellation theory, Proc. Lond. Math. Soc. (3) 84(3) (2002), 599–644.CrossRefGoogle Scholar
McCammond, J. P. and Wise, D. T., Coherence, local quasiconvexity, and the perimeter of 2-complexes, Geom. Funct. Anal. 15(4) (2005), 859–927.CrossRefGoogle Scholar
Scott, G. P., Finitely generated 3-manifold groups are finitely presented, J. Lond. Math. Soc. (2) 6 (1973), 437–440.CrossRefGoogle Scholar
Sieradski, A. J., A coloring test for asphericity, Q. J. Math. Oxford Ser. (2) 34(133) (1983), 97–106.CrossRefGoogle Scholar
Stallings, J., Coherence of 3-manifold fundamental groups, in Séminaire Bourbaki, Vol. 1975/76, 28 ème année, Exp. No. 481, Lecture Notes in Mathematics, Volume 567, pp. 167–173 (Springer, Berlin, 1977).CrossRefGoogle Scholar
Wise, D. T., On the vanishing of the 2nd $L^{2}$ betti number. Available at http://www.math.mcgill.ca/wise/papers, pp. 1–21, submitted.Google Scholar
Wise, D. T., The structure of groups with a quasiconvex hierarchy, Ann. Math. Stud. 209 (2021), to appear.Google Scholar
Wise, D. T., Sectional curvature, compact cores, and local quasiconvexity, Geom. Funct. Anal. 14(2) (2004), 433–468.10.1007/s00039-004-0463-xCrossRefGoogle Scholar
Wise, D. T., The coherence of one-relator groups with torsion and the Hanna Neumann conjecture, Bull. Lond. Math. Soc. 37(5) (2005), 697–705.CrossRefGoogle Scholar
Wise, D. T., Nonpositive sectional curvature for (p, q, r)-complexes, Proc. Amer. Math. Soc. 136(1) (2008), 41–48 (electronic).10.1090/S0002-9939-07-08921-6CrossRefGoogle Scholar