Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-23T02:05:57.376Z Has data issue: false hasContentIssue false
  • English
  • Français

BOUNDNESS OF INTERSECTION NUMBERS FOR ACTIONS BY TWO-DIMENSIONAL BIHOLOMORPHISMS

Part of: Special aspects of infinite or finite groups Complex dynamical systems Linear algebraic groups and related topics Holomorphic mappings and correspondences Smooth dynamical systems: general theory

Published online by Cambridge University Press:  22 January 2021

Javier Ribón Open the ORCID record for Javier Ribón [Opens in a new window]
Javier Ribón*
Affiliation:
Instituto de Matemática e Estatística, Universidade Federal Fluminense, Campus do Gragoatá, Rua Marcos Valdemar de Freitas Reis s/n, 24210-201 Niterói, Rio de Janeiro, Brazil ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We say that a group G of local (maybe formal) biholomorphisms satisfies the uniform intersection property if the intersection multiplicity 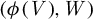$(\phi (V), W)$ takes only finitely many values as a function of G for any choice of analytic sets V and W of complementary dimension. In dimension 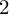$2$ we show that G satisfies the uniform intersection property if and only if it is finitely determined – that is, if there exists a natural number k such that different elements of G have different Taylor expansions of degree k at the origin. We also prove that G is finitely determined if and only if the action of G on the space of germs of analytic curves has discrete orbits.

Keywords

local diffeomorphismintersection numbersolvable groupnilpotent group

MSC classification

Primary: 32H50: Iteration problems 37C85: Dynamics of group actions other than ${bf Z}$ and ${bf R}$, and foliations
Secondary: 37F75: Holomorphic foliations and vector fields 20G20: Linear algebraic groups over the reals, the complexes, the quaternions 20F16: Solvable groups, supersolvable groups
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 21 , Issue 5 , September 2022 , pp. 1677 - 1700
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arnold, V. I., Dynamics of complexity of intersections, Bol. Soc. Bras. Mat., Nova Sér., 21(1) (1990), 1–10.CrossRefGoogle Scholar
Arnold, V. I., Dynamics of intersections, in Analysis, et Cetera, pp. 77–84 (Academic Press, Boston, MA, 1990).CrossRefGoogle Scholar
Arnold, V. I., ed., Arnold’s Problems (Springer, Berlin, 2004). Translated and revised edition of the 2000 Russian original.Google Scholar
Arnold, V. I., Bounds for Milnor numbers of intersections in holomorphic dynamical systems, in Topological Methods in Modern Mathematics: Proceedings of a Symposium in Honor of John Milnor’s Sixtieth Birthday, Held at the State University of New York at Stony Brook , USA, June 14-June 21, 1991, pp. 379–390 (Publish or Perish, Inc., Houston, TX, 1993).Google Scholar
Artin, M. and Mazur, B., On periodic points, Ann. of Math. (2) 81 (1965), 82–99.Google Scholar
Baouendi, M. S., Preiss Rothschild, L., Winkelmann, J. and Zaitsev, D., Lie group structures on groups of diffeomorphisms and applications to CR manifolds, Ann. Inst. Fourier (Grenoble), 54(5) (2004), 1279–1303, 2004.Google Scholar
Binyamini, G., Finiteness properties of formal Lie group actions, Transform. Groups, 20(4) (2015), 939–952.Google Scholar
Borel, A., Linear Algebraic Groups , 2nd ed., Graduate Texts in Mathematics no. 126, (Springer-Verlag, New York, 1991.Google Scholar
Casas-Alvero, E., Singularities of Plane Curves (Cambridge University Press, 2000).Google Scholar
Cerveau, D. and Mattei, J.-F., Formes intégrables holomorphes singulières, Astèrisque, 97:(1982).Google Scholar
Écalle, J., Théorie itérative: introduction à la théorie des invariants holomorphes, J.Math. Pures Appl. (9) 54 (1975), 183–258.Google Scholar
Favre, C. and Jonsson, M., The Valuative Tree Lecture Notes in Mathematics no. 1853 (Springer-Verlag, Berlin, 2004).Google Scholar
Fulton, W., Intersection Theory, 2nd ed. (Springer, Berlin, 1998).Google Scholar
Ilyashenko, Y. and Yakovenko, S., Lectures on Analytic Differential Equations Graduate Studies in Mathematics no. 86 (American Mathematical Society, Providence, RI, 2008).Google Scholar
Levy, A., Basic Set Theory (Dover Publications, Mineola, NY, 2002). Reprint of the 1979 original.Google Scholar
Martelo, M. and Ribón, J., Derived length of solvable groups of local diffeomorphisms, Math. Ann. 358(3) (2014), 701–728.CrossRefGoogle Scholar
Martinet, J. and Ramis, J.-P., Classification analytique des équations differentielles non linéaires résonnantes du premier ordre, Ann. Sci. ÈEc. Norm. Supèr. (4), 4(16) (1983), 571–621.Google Scholar
Mattei, J. -F. and Moussu, R., Holonomie et intégrales premières, Ann. Sci. Èc. Norm. Supèr. (4), 13(4) (1908), 469–523.CrossRefGoogle Scholar
Ribón, J., Finite dimensional groups of local diffeomorphisms, Israel J.Math. 227(1) (2018), 289–329.Google Scholar
Ribón, J., The solvable length of groups of local diffeomorphisms, J.Reine Angew. Math. 752 (2019), 105–139.CrossRefGoogle Scholar
Seigal, A. L. and Yakovenko, S., Local dynamics of intersections: V. I. Arnold’s theorem revisited, Israel J.Math. 201(2) (2014), 813–833.CrossRefGoogle Scholar
Shastri, A. R., Elements of Differential Topology (CRC Press, Boca Raton, FL, 2011). With a foreword by F. T. Farrell.CrossRefGoogle Scholar
Shub, M. and Sullivan, D., A remark on the Lefschetz fixed point formula for differentiable maps, Topology 13 (1974), 189–191.Google Scholar
Skolem, T., Ein Verfahren zur Behandlung gewisser exponentialer Gleichungen und diophantischer Gleichungen, in 8th Scand. Math. Congr., Stockholm, 1934, pp. 163–188 (Håkan Ohlssons Boktryckeri, Lund, 1935).Google Scholar
Wall, C. T. C., Singular Points of Plane Curves, London Mathematical Society Student Texts no. 63 (Cambridge University Press, 2004).Google Scholar