Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-17T16:01:51.844Z Has data issue: false hasContentIssue false
  • English
  • Français

Boundaries of instability zones for symplectic twist maps

Part of: Low-dimensional dynamical systems

Published online by Cambridge University Press:  08 February 2013

M.-C. Arnaud
M.-C. Arnaud*
Affiliation:
Université d’Avignon et des Pays de Vaucluse, Laboratoire d’Analyse non linéaire et Géométrie (EA 2151), F-84018 Avignon, France ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Very few things are known about the curves that are at the boundary of the instability zones of symplectic twist maps. It is known that in general they have an irrational rotation number and that they cannot be KAM curves. We address the following questions. Can they be very smooth? Can they be non-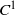${C}^{1} $?

Can they have a Diophantine or a Liouville rotation number? We give a partial answer for 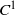${C}^{1} $ and 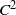${C}^{2} $ twist maps.

In Theorem 1, we construct a 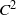${C}^{2} $ symplectic twist map 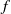$f$ of the annulus that has an essential invariant curve 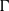$\Gamma $ such that

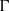$\bullet $ $\Gamma $ is not differentiable;

$\bullet $ the dynamics of 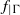${f}_{\vert \Gamma } $ is conjugated to the one of a Denjoy counter-example;

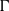$\bullet $ $\Gamma $ is at the boundary of an instability zone for 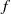$f$.

Using the Hayashi connecting lemma, we prove in Theroem 2 that any symplectic twist map restricted to an essential invariant curve can be embedded as the dynamics along a boundary of an instability zone for some 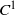${C}^{1} $ symplectic twist map.

Keywords

twist mapsinstability zonesinvariant curvesirregularity of invariant curvesDenjoy counter-examplesconnecting lemma

MSC classification

Secondary: 37E40: Twist maps 37E10: Maps of the circle
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 13 , Issue 1 , January 2014 , pp. 19 - 41
Copyright
©Cambridge University Press 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arnaud, M.-C., A non-differentiable essential irrational invariant curve for a ${C}^{1} $ symplectic twist map, J. Mod. Dyn. 5 (3) (2011), 583–591.Google Scholar
Arnaud, M.-C., Bonatti, C. and Crovisier, S., Dynamiques symplectiques génériques, Ergodic Theory Dynam. Systems 25 (5) (2005), 1401–1436.Google Scholar
Arnol’d, V, Proof of a theorem of A. N. Kolmogorov on the preservation of conditionally periodic motions under a small perturbation of the Hamiltonian, Uspekhi Mat. Nauk 18 (5(113)) (1963), 13–40 (in Russian).Google Scholar
Aubry, S., The twist map, the extended Frenkel–Kontorova model and the devil’s staircase, Order in chaos (Los Alamos, N.M., 1982), Physica D 7 (1–3) (1983), 240–258.Google Scholar
Birkhoff, G. D., Surface transformations and their dynamical application, Acta Math. 43 (1920), 1–119.Google Scholar
Birkhoff, G. D., Sur l’existence de régions d’instabilité en Dynamique, Ann. Inst. H. Poincaré 2 (4) (1932), 369–386.Google Scholar
Chenciner, A., La dynamique au voisinage d’un point fixe elliptique conservatif: de Poincaré et Birkhoff à Aubry et Mather [The dynamics at the neighborhood of a conservative elliptic fixed point: from Poincaré and Birkhoff to Aubry and Mather], Seminar Bourbaki, Volume 1983/84, Astérisque 121–122 (1985), 147–170 (in French).Google Scholar
Douady, R., Applications du théorème des tores invariants, PhD thesis, Univ. Paris 7 (1982).Google Scholar
Forni, G. and Mather, J. N., Action minimizing orbits in Hamiltonian systems, in Transition to chaos in classical and quantum mechanics (Montecatini Terme, 1991), Lecture Notes in Math., Volume 1589, pp. 92–186 (Springer, Berlin, 1994).Google Scholar
Golé, C., Symplectic twist maps. Global variational techniques, Advanced Series in Nonlinear Dynamics, Volume 18 (World Scientific Publishing Co., Inc., River Edge, NJ, 2001).Google Scholar
Hayashi, S., Connecting invariant manifolds and the solution of the ${C}^{1} $ stability and $\Omega $-stability conjectures for flows, Ann. of Math. (2) 145 (1) (1997), 81–137.Google Scholar
Herman, M., Sur les courbes invariantes par les difféomorphismes de l’anneau, Vol. 1, Asterisque, 103–104 (Société Mathématique de France, Paris, 1983).Google Scholar
Hirsch, M. W., Differential topology, Graduate Texts in Mathematics, Volume 33 (Springer-Verlag, New York–Heidelberg, 1976), x+221 pp.Google Scholar
Kolmogorov, A. N., On conservation of conditionally periodic motions for a small change in Hamilton’s function, Dokl. Akad. Nauk SSSR (N.S.) 98 (1954), 527–530 (in Russian).Google Scholar
Le Calvez, P., Propriétés dynamiques des régions d’instabilité [Dynamical properties of regions of instability], Ann. Sci. Éc. Norm. Super. (4) 20 (3) (1987), 443–464 (in French).Google Scholar
MacKay, R. S. and Percival, I. C., Converse KAM: theory and practice, Comm. Math. Phys. 98 (4) (1985), 469–512.Google Scholar
Mather, J. N., Glancing billiards, Ergodic Theory Dynam. Systems 2 (3–4) (1983), 397–403.Google Scholar
Mather, J. N., Nonexistence of invariant circles, Ergodic Theory Dynam. Systems 4 (2) (1984), 301–309.Google Scholar
Mather, J. N., Variational construction of orbits of twist diffeomorphisms, J. Amer. Math. Soc. 4 (2) (1991), 207–263.Google Scholar
Moser, J. N., On invariant curves of area-preserving mappings of an annulus, Nachr. Akad. Wiss. Göttingen Math.-Phys. Kl. II 1–20 (1962).Google Scholar
Pugh, C. C. and Robinson, C., The ${C}^{1} $ closing lemma, including Hamiltonians, Ergodic Theory Dynam. Systems 3 (2) (1983), 261–313.CrossRefGoogle Scholar
Robinson, C., Generic properties of conservative systems, Amer. J. Math. 92 (1970), 562–603.Google Scholar
Rüssman, H., On the existence of invariant curves of twist mappings of an annulus, in Geometric dynamics (Rio de Janeiro, 1981), Lecture Notes in Math., Volume 1007, pp. 677–718 (Springer, Berlin, 1983).Google Scholar