Hostname: page-component-669899f699-7tmb6 Total loading time: 0 Render date: 2025-04-25T16:29:06.865Z Has data issue: false hasContentIssue false
  • English
  • Français

ACTIONS OF AUTOMORPHISM GROUPS OF FREE GROUPS ON SPACES OF JACOBI DIAGRAMS. II

Part of: Special aspects of infinite or finite groups

Published online by Cambridge University Press:  09 June 2022

Mai Katada Open the ORCID record for Mai Katada [Opens in a new window]
Mai Katada*
Affiliation:
Department of Mathematics, Kyoto University, Kyoto 606-8502, Japan
*
[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The automorphism group 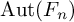$\operatorname {Aut}(F_n)$ of the free group 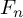$F_n$ acts on a space 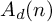$A_d(n)$ of Jacobi diagrams of degree d on n oriented arcs. We study the 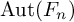$\operatorname {Aut}(F_n)$-module structure of 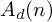$A_d(n)$ by using two actions on the associated graded vector space of 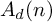$A_d(n)$: an action of the general linear group 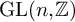$\operatorname {GL}(n,\mathbb {Z})$ and an action of the graded Lie algebra 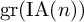$\mathrm {gr}(\operatorname {IA}(n))$ of the IA-automorphism group 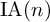$\operatorname {IA}(n)$ of 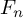$F_n$ associated with its lower central series. We extend the action of 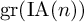$\mathrm {gr}(\operatorname {IA}(n))$ to an action of the associated graded Lie algebra of the Andreadakis filtration of the endomorphism monoid of 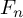$F_n$. By using this action, we study the 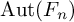$\operatorname {Aut}(F_n)$-module structure of 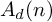$A_d(n)$. We obtain an indecomposable decomposition of 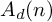$A_d(n)$ as 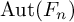$\operatorname {Aut}(F_n)$-modules for $n\geq 2d$. Moreover, we obtain the radical filtration of 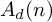$A_d(n)$ for $n\geq 2d$ and the socle of 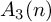$A_3(n)$.

Keywords

Jacobi diagramsautomorphism groups of free groupsgeneral linear groupsIA-automorphism groups of free groupsAndreadakis filtration

MSC classification

Primary: 20F12: Commutator calculus
Secondary: 20F28: Automorphism groups of groups
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 23 , Issue 1 , January 2024 , pp. 1 - 69
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Andreadakis, S., ‘On the automorphisms of free groups and free nilpotent groups’, Proc. London Math. Soc. (3) 15 (1965), 239–268. https://londmathsoc.onlinelibrary.wiley.com/doi/abs/10.1112/plms/s3-15.1.239.CrossRefGoogle Scholar
Bar-Natan, D., ‘On the Vassiliev knot invariants’, Topology 34(2) (1995), 423–472. https://www.sciencedirect.com/science/article/pii/0040938395932372?via.CrossRefGoogle Scholar
Bar-Natan, D., ‘Vassiliev homotopy string link invariants’, J. Knot Theory Ramifications 4(1) (1995), 13–32. https://www.worldscientific.com/doi/abs/10.1142/ S021821659500003X.CrossRefGoogle Scholar
Bar-Natan, D., ‘Some computations related to Vassiliev invariants,’ Preprint, 1996.Google Scholar
Bartholdi, L., ‘Automorphisms of free groups I—erratum’, New York J. Math. 22 (2016), 1135–1137 [MR3084710]. https://nyjm.albany.edu/j/2016/22-52.html.Google Scholar
Fulton, W., Young Tableaux, London Mathematical Society Student Texts, Vol. 35 (Cambridge University Press, Cambridge, 1997).Google Scholar
Fulton, W. and Harris, J., Representation Theory A First Course, Readings in Mathematics, Graduate Texts in Mathematics, Vol. 129 (Springer-Verlag, New York, 1991).Google Scholar
Habegger, N. and Lin, X.-S., ‘The classification of links up to link-homotopy’, J. Amer. Math. Soc. 3(2) (1990), 389–419. https://www.ams.org/journals/jams/1990-03-02/S0894-0347-1990-1026062-0/home.html.CrossRefGoogle Scholar
Habiro, K., ‘Bottom tangles and universal invariants’, Algebr. Geom. Topol. 6 (2006), 1113–1214. https://msp.org/agt/2006/6-3/p05.xhtml.CrossRefGoogle Scholar
Habiro, K. and Massuyeau, G., ‘Generalized Johnson homomorphisms for extended N-series’, J. Algebra 510 (2018), 205–258. https://www.sciencedirect.com/ science/article/pii/S0021869318303569?via.CrossRefGoogle Scholar
Habiro, K. and Massuyeau, G., ‘The Kontsevich integral for bottom tangles in handlebodies’, Quantum Topol. 12(4) (2021), 593–703. https://mathscinet.ams.org/mathscinet-getitem?mr=4321214.CrossRefGoogle Scholar
Hartl, M., Pirashvili, T. and Vespa, C., ‘Polynomial functors from algebras over a set-operad and nonlinear Mackey functors’, Int. Math. Res. Not. IMRN 6 (2015), 1461–1554. https://academic.oup.com/imrn/article/2015/6/1461/668187.CrossRefGoogle Scholar
Hinich, V. and Vaintrob, A., ‘Cyclic operads and algebra of chord diagrams’, Selecta Math. (N.S.) 8(2) (2002), 237–282. https://doi.org/10.1007/s00029-002-8106-2.CrossRefGoogle Scholar
James, G. and Kerber, A., The Representation Theory of the Symmetric Group, Encyclopedia of Mathematics and its Applications, Vol. 16 (Addison-Wesley Publishing Co., Reading, Mass., 1981), With a foreword by P. M. Cohn and an introduction by Gilbert de B. Robinson.Google Scholar
Kassel, C., Quantum Groups, Graduate Texts in Mathematics, Vol. 155 (Springer-Verlag, New York, 1995).CrossRefGoogle Scholar
Katada, M., ‘Actions of automorphism groups of free groups on spaces of Jacobi diagrams, I’, Ann. Inst. Fourier (2021) (to appear), Preprint, arXiv: 2102.06382. https://arxiv.org/bs/2102.06382.Google Scholar
Kawazumi, N., ‘Cohomological aspects of Magnus expansions’, Preprint, 2005, arXiv: math/0505497. https://arxiv.org/abs/math/0505497.Google Scholar
Kontsevich, M., ‘Vassiliev’s knot invariants’, In I. M. Gel’fand Seminar, Adv. Soviet Math., Vol. 16 (Amer. Math. Soc., Providence, RI, 1993), 137–150.CrossRefGoogle Scholar
Ohtsuki, T., Quantum Invariants, Series on Knots and Everything, Vol. 29 (World Scientific Publishing Co., Inc., River Edge, NJ, 2002).Google Scholar
Powell, G. and Vespa, C., ‘Higher Hochschild homology and exponential functors’, Preprint, 2018, arXiv: 1802.07574. https://arxiv.org/abs/1802.07574.Google Scholar
Sagan, B. E., The Symmetric Group, 2nd ed., Graduate Texts in Mathematics, Vol. 203 (Springer-Verlag, New York, 2001).CrossRefGoogle Scholar
Satoh, T., ‘A survey of the Johnson homomorphisms of the automorphism groups of free groups and related topics’, In Handbook of Teichmüller theory. Vol. V, IRMA Lect. Math. Theor. Phys., Vol. 26 (Eur. Math. Soc., Zürich, 2016), 167–209. https://arxiv.org/abs/1204.0876.CrossRefGoogle Scholar
Satoh, T., ‘The third subgroup of the Andreadakis-Johnson filtration of the automorphism group of a free group’, J. Group Theory 22(1) (2019), 41–61. https://www.degruyter.com/document/doi/10.1515/jgth-2018-0037/html.CrossRefGoogle Scholar