Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-23T10:35:26.097Z Has data issue: false hasContentIssue false
  • English
  • Français

Uniqueness of non-negative internal rate of return

Published online by Cambridge University Press:  20 April 2012

Allen M. Russell  and
John A. Rickard
Get access Rights & Permissions [Opens in a new window]

Extract

We will be considering a productive investment project or financial security which yields a sequence of cash flows, positive or negative, over time. Let a1 (dollars) be the cash flow from the project at time t, where t takes the values 0, 1, 2,…, n. Given the known cash flows at from the project, and a known market rate of interest, i per period, at which money may be borrowed or invested, a common procedure is to accept the project if its present value P is greater than zero, where

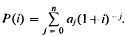
An internal rate of return of the project is defined to be a solution of the equation

in (− 1, ∞), if, of course, one exists.

Type
Research Article
Information
Journal of the Institute of Actuaries , Volume 109 , Issue 3 , December 1982 , pp. 435 - 445
Copyright
Copyright © Institute and Faculty of Actuaries 1982

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

(1) Aucamp, D. C. & Eckardt, W. L. Jr (1976) A sufficient condition for a unique non-negative internal rate of return-comment. J. Fin. Quant. Anal. 11: 2 (June), 329–32.CrossRefGoogle Scholar
(2) Bernhard, R. H. (1967) On the inconsistency of the Soper and Sturm–Kaplan conditions for uniqueness of the internal rate of return. J. Indust. Eng. 18:8 (August), 498–500.Google Scholar
(3) Bernhard, R. H. (1971) A comprehensive comparison and critique of discounting indices proposed for capital investment evaluation. Eng. Econ. 16:3 (Spring), 157–86.CrossRefGoogle Scholar
(4) Bernhard, R. H. (1979) A more general sufficient condition for a unique non-negative internal rate of return. J. Fin. Quant. Anal. 14:2 (June), 337–41.CrossRefGoogle Scholar
(5) Bernhard, R. H. (1980) A simplification and an extension of the Bernhard–de Faro sufficient condition for a unique non-negative internal rate of return. J. Fin. Quant. Anal. 15:1 (March), 201–9.CrossRefGoogle Scholar
(6) De Faro, C. (1973) A sufficient condition for a unique non-negative internal rate of return. J. Fin. Quant. Anal. 8:4 (September), 683–4.CrossRefGoogle Scholar
(7) De Faro, C. (1978) A sufficient condition for a unique non-negative internal rate of return: further comments. J. Fin. Quant. Anal. 13:3 (September), 577–84.CrossRefGoogle Scholar
(8) Kaplan, S. (1965) A note on a method for precisely determining the uniqueness or non-uniqueness of the internal rate of return for a proposed investment. J. Indust. Eng. 16:1 (January/February), 70–1.Google Scholar
(9) Norstrøm, C. J. (1972) A sufficient condition for a unique non-negative internal rate of return. J. Fin. Quant. Anal. 7:3 (June), 1835–9.CrossRefGoogle Scholar
(10) Soper, C. S. (1959) The marginal efficiency of capital: a further note. Econ. J. 69:273 (March), 174–7.Google Scholar