No CrossRef data available.
Article contents
On the Value of Annuities payable Half-yearly, Quarterly, &c. (Part II)
Published online by Cambridge University Press: 18 August 2016
Extract
In the last Number of this Journal I examined and compared the solutions of this question given by Milne, Baily, and Griffith Davies in their standard works. The first of these writers cannot be considered to have treated the question in a satisfactory manner. The two latter have investigated the problem more rigorously. They both proceed upon the supposition commonly adopted, viz. that the deaths occurring in each year of age are distributed uniformly over the year. They differ, however, in their views as to the interest to be allowed for fractions of a year, Davies throughout adopting Milne's view, by which the present value of £1 due in six months' time is 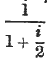 , while Baily takes the value as
, while Baily takes the value as 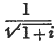 . The latter, as I have already stated, appears to me the preferable view. Davies, however, has also given an investigation of the value of an annuity payable m times a year, on the supposition that interest is convertible into principal m times in the year; and his solution, as I have shown in the last Number of the Journal, is substantially the same as Baily's.
. The latter, as I have already stated, appears to me the preferable view. Davies, however, has also given an investigation of the value of an annuity payable m times a year, on the supposition that interest is convertible into principal m times in the year; and his solution, as I have shown in the last Number of the Journal, is substantially the same as Baily's.
- Type
- Research Article
- Information
- Copyright
- Copyright © Institute and Faculty of Actuaries 1867
References
page 202 note * There is in Professor De Morgan's paper what appears to me, if not an error, at least an ambiguity, of language. He says (p. 138), “If the mortality of the table be increasing from year to year, it ought to be supposed that the mortality of the latter part of a year is greater than that of the former.” The meaning of this is not, as might be supposed at first sight, “If the rate of mortality be increasing,” &c.; but from the context it appears that the meaning intended is, “If the number dying in a year be increasing from year to year, it ought to be supposed that the number dying in the latter part of the year is greater than the number dying in the former part.” I should be glad to learn whether the learned author, on reflection, considers that his words accurately express his meaning.
page 207 note * If the difference between successive values of a be h instead of 1, this formula becomes

Compare the formulæ given by Mr. Woolhouse. vol. XL, pp. 317, 331.


