Published online by Cambridge University Press: 18 August 2016
Before proceeding to a description of the formulas which form the main subject of this paper, it will be worth while to notice some points in connection with the celebrated “Summation Formula” of Maclaurin, the application of which to life contingencies we owe to Mr. Woolhouse. As Mr. Sutton has shown (J.I.A. xv, p. 307), the formula in question may be very simply established by symbolical methods. Thus, putting D for  , we have
, we have
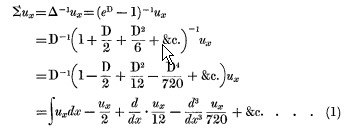
If we transpose the quantities ∑Ux and ∫uxdx, we get an expression for the value of the integral in terms of the sum of the function; and inserting the limits of integration, we obtain

Assuming, as in life calculations, that everything vanishes at the upper limit, we have

This important formula, which in practice is very powerful, is usually, at first, rapidly convergent, but ultimately becomes divergent. It has been shown, however, that the convergent portion will always give approximate numerical results. The main reason for reproducing the above demonstration, which will be familiar to most readers, is to show how, by a similar method, we may arrive at another summation formula, slightly more convergent than (1).
page 97 note * A very convenient expression for calculating this function.