No CrossRef data available.
Article contents
An Improved Method of Approximating to the Value of Annuities involving Three Lives
Published online by Cambridge University Press: 18 August 2016
Extract
The ordinary method of approximating to three-life annuities is as follows:—Let the lives be aged respectively x, y, z, (x being the youngest). Find an age w such that at the given rate of interest aw=ayz, then axyz=axw nearly. Baily diminishes the value thus found by .05, but I cannot say if this correction is usually made. It will generally be found to be too small if the lives are very young, but much too large at the older ages.
It has been shown that the above method (neglecting now the correction referred to) is strictly accurate in any mortality table where the mortality conforms to Mr. Gompertz's hypothesis, and where consequently the force of mortality can be represented throughout by the expression
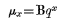
(B and q being constants). The reason for this is, that the force of mortality for two joint lives, or, x, x + t, may be represented by a similar expression
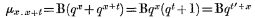
(where qt′ = qt + 1).
It follows from this that if we have
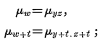
we have also
and, the force of mortality in the joint status being equal to that for the single life, throughout the table, the two annuities are identical, not only as to their total value, but also as to the value of each successive payment.
- Type
- Research Article
- Information
- Copyright
- Copyright © Institute and Faculty of Actuaries 1882
References
page 275 note * We have obtained the following information as to the practice on this point of 24 offices in London and Edinburgh. Seven offices, in applying Simpson's rule, make the correction of –·05; and one other makes it only when the lives upon which the annuity depends, are over 60 years of age. Twelve offices use Simpson's rule without the correction. Two use the following modification of Simpson's rule, devised by Mr. Meikle:—
where a r−1 > aw > ar , r being the integral age nest above w. (This formula is given and explained in a paper on Joint Life Annuities, by Mr. J. J. HeLauchlan, in the Transactions of the Actuarial Society of Edinburgh, New Series, No. 2.) One office has adopted the tables appended to Messrs. King and Hardy's paper on the Practical Application of Mr. Makeham's Formula to the Graduation of Mortality Tables (J.I.A., xxii, 191). One office calculates the values of annuities on three joint lives by means of Mr. Woolhouse's formula (D) (J.I.A., xi, 321).
The correction of −·05, although attributed to Baily by D. Jones, appears to have been originally suggested by Price. See his Observations on Reversionary Payments, 7th edition, vol. ii, p. 366.—ED. J.I.A.
page 283 note * Mr. Hardy states that the value of A used by him is obtained from the constants given in the joint paper by Messrs. King and Hardy, on Mr, Makeham's formula (Journal, vol. xxii, p. 191).—ED. J.I.A.