In the last Number of this Journal I examined and compared the solutions of this question given by Milne, Baily, and Griffith Davies in their standard works. The first of these writers cannot be considered to have treated the question in a satisfactory manner. The two latter have investigated the problem more rigorously. They both proceed upon the supposition commonly adopted, viz. that the deaths occurring in each year of age are distributed uniformly over the year. They differ, however, in their views as to the interest to be allowed for fractions of a year, Davies throughout adopting Milne's view, by which the present value of £1 due in six months' time is 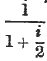, while Baily takes the value as 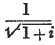. The latter, as I have already stated, appears to me the preferable view. Davies, however, has also given an investigation of the value of an annuity payable m times a year, on the supposition that interest is convertible into principal m times in the year; and his solution, as I have shown in the last Number of the Journal, is substantially the same as Baily's.