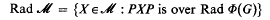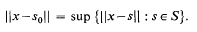Research Article
Rings related to completely 0-simple semigroups
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 257-274
-
- Article
-
- You have access
- Export citation
Identical relations in loops, I
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 275-286
-
- Article
-
- You have access
- Export citation
On Finite Groups With ‘Hidden’ Primes
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 287-300
-
- Article
-
- You have access
- Export citation
On Exposed and Farthest Points in Normed Linear Spaces
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 301-308
-
- Article
-
- You have access
- Export citation
Simplexes Self-Polar for a Simplex
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 309-314
-
- Article
-
- You have access
- Export citation
Asymptotic Gauss Quadrature Errors as Fourier Coefficients of the Integrand1
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 315-322
-
- Article
-
- You have access
- Export citation
Congruences on Orthodox Semigroups
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 323-341
-
- Article
-
- You have access
- Export citation
On the Unicellularity of Weighted Shifts
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 342-350
-
- Article
-
- You have access
- Export citation
Groups of Matrices With Integer Eigenvalues
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 351-357
-
- Article
-
- You have access
- Export citation
On Finitely Generated Subgroups of Free Products
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 358-364
-
- Article
-
- You have access
- Export citation
A Graphical Exposition of the Ising Problem1
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 365-377
-
- Article
-
- You have access
- Export citation
Some Results on Configurations
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 378-384
-
- Article
-
- You have access
- Export citation
Front matter
JAZ volume 12 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
JAZ volume 12 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation