Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-23T23:30:50.287Z Has data issue: false hasContentIssue false
  • English
  • Français

WORDS AND PRONILPOTENT SUBGROUPS IN PROFINITE GROUPS

Part of: Structure and classification of infinite or finite groups Special aspects of infinite or finite groups Representation theory of groups

Published online by Cambridge University Press:  29 September 2014

E. I. KHUKHRO  and
P. SHUMYATSKY
E. I. KHUKHRO*
Affiliation:
Sobolev Institute of Mathematics, Novosibirsk 630 090, Russia email [email protected]
P. SHUMYATSKY
Affiliation:
Department of Mathematics, University of Brasilia, Brasilia DF 70910-900, Brazil email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

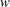Let $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}w$ be a multilinear commutator word, that is, a commutator of weight $n$ in $n$ different group variables. It is proved that if 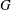$G$ is a profinite group in which all pronilpotent subgroups generated by 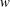$w$-values are periodic, then the verbal subgroup 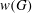$w(G)$ is locally finite.

Keywords

profinite groupslocally finitecommutatorpronilpotentperiodic

MSC classification

Secondary: 20E18: Limits, profinite groups 20D10: Solvable groups, theory of formations, Schunck classes, Fitting classes, $pi$-length, ranks 20D20: Sylow subgroups, Sylow properties, $pi$-groups, $pi$-structure 20F50: Periodic groups; locally finite groups
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 97 , Issue 3 , December 2014 , pp. 343 - 364
Copyright
Copyright © 2014 Australian Mathematical Publishing Association Inc. 

References

Acciarri, C. and Shumyatsky, P., ‘On profinite groups in which commutators are covered by finitely many subgroups’, Math. Z. 274 (2013), 239–248.Google Scholar
Berger, T. R. and Gross, F., ‘2-length and the derived length of a Sylow 2-subgroup’, Proc. Lond. Math. Soc. (3) 34 (1977), 520–534.Google Scholar
Bryukhanova, E. G., ‘The 2-length and 2-period of a finite solvable group’, Algebra Logika 18 (1979), 9–31; (English translation), Algebra Logic 18 (1979), 5–20.Google Scholar
Bryukhanova, E. G., ‘The relation between 2-length and derived length of a Sylow 2-subgroup of a finite soluble group’, Mat. Zametki 29(2) (1981), 161–170; (English translation), Math. Notes 29(1–2) (1981), 85–90.Google Scholar
Detomi, E., Morigi, M. and Shumyatsky, P., Bounding the exponent of a verbal subgroup, Ann. Mat. Pura Appl., to appear; doi:10.1007/s10231-013-0336-8.CrossRefGoogle Scholar
Detomi, E., Morigi, M. and Shumyatsky, P., Commutators and pronilpotent subgroups in profinite groups, Monatsh. Math., to appear; doi:10.1007/s00605-013-0538-6, arXiv:1305.5351.Google Scholar
Detomi, E., Morigi, M. and Shumyatsky, P., On countable coverings of word values in profinite groups, J. Pure Appl. Algebra, to appear; doi:10.1016/j.jpaa.2014.05.030, arXiv:1309.0636.CrossRefGoogle Scholar
Feit, W. and Thompson, J. G., ‘Solvability of groups of odd order’, Pacific J. Math. 13 (1963), 773–1029.Google Scholar
Gorenstein, D., Finite Groups (Chelsea, New York, 1980).Google Scholar
Gross, F., ‘The 2-length of a finite solvable group’, Pacific J. Math. 15 (1965), 1221–1237.CrossRefGoogle Scholar
Hall, P. and Higman, G., ‘The p-length of a p-soluble group and reduction theorems for Burnside’s problem’, Proc. Lond. Math. Soc. (3) 6 (1956), 1–42.Google Scholar
Herfort, W., ‘Compact torsion groups and finite exponent’, Arch. Math. 33 (1979), 404–410.Google Scholar
Hoare, A. H. M., ‘A note on 2-soluble groups’, J. Lond. Math. Soc. 35 (1960), 193–199.CrossRefGoogle Scholar
Jones, G. A., ‘Varieties and simple groups’, J. Aust. Math. Soc. 17 (1974), 163–173.Google Scholar
Kelley, J. L., General Topology (Van Nostrand, Toronto–New York–London, 1955).Google Scholar
Khukhro, E. I. and Shumyatsky, P., Nonsoluble and non-$p$-soluble length of finite groups, Israel J. Math., to appear; arXiv:1310.2434.Google Scholar
Mann, A., ‘The exponent of central factors and commutator groups’, J. Group Theory 10 (2007), 435–436.Google Scholar
Mazurov, V. D. and Khukhro, E. I. (eds.) . The Kourovka Notebook. Unsolved Problems in Group Theory, 17th edn (Institute of Mathematics, Novosibirsk, 2010).Google Scholar
Shumyatsky, P., ‘Centralizers in groups with finiteness conditions’, J. Group Theory 1 (1998), 275–282.Google Scholar
Shumyatsky, P., ‘Verbal subgroups in residually finite groups’, Quart. J. Math. 51 (2000), 523–528.Google Scholar
Shumyatsky, P., ‘On profinite groups in which commutators are Engel’, J. Aust. Math. Soc. 70 (2001), 1–9.Google Scholar
Shumyatsky, P., ‘On the exponent of a verbal subgroup in a finite group’, J. Aust. Math. Soc. 93 (2012), 325–332.Google Scholar
Thompson, J., ‘Automorphisms of solvable groups’, J. Algebra 1 (1964), 259–267.Google Scholar
Turull, A., ‘Character theory and length problems’, in: Finite and Locally Finite Groups, NATO ASI Series, 471 (Kluwer Academic, Dordrecht–Boston–London, 1995), 377–400.Google Scholar
Wilson, J., ‘On the structure of compact torsion groups’, Monatsh. Math. 96 (1983), 57–66.CrossRefGoogle Scholar
Wilson, J., Profinite Groups (Clarendon Press, Oxford, 1998).CrossRefGoogle Scholar
Zelmanov, E. I., ‘On periodic compact groups’, Israel J. Math. 77(1–2) (1992), 83–95.CrossRefGoogle Scholar