Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-27T22:57:27.848Z Has data issue: false hasContentIssue false
  • English
  • Français

Weighted composition operators in weighted Banach spaces of analytic functions

Part of: Entire and meromorphic functions, and related topics Linear function spaces and their duals Special classes of linear operators

Published online by Cambridge University Press:  09 April 2009

M. D. Contreras  and
A. G. Hernandez-Diaz
A. G. Hernandez-Diaz
Affiliation:
Departmento de Matem´tica Aplicada II Escuela Superior de Ingenieros Universidad de SevillaCamino de los Descubrimientos, s/n 41092, SevillaSpain e-mail: [email protected] e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

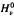We characterize the boundedness and compactness of weighted composition operators between weighted Banach spaces of analytic functions and 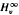. we estimate the essential norm of a weighted composition operator and compute it for those Banach spaces 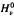which are isomorphic to c0. We also show that, when such an operator is not compact, it is an isomorphism on a subspace isomorphic to c0 or l∞. Finally, we apply these results to study composition operators between Bloch type spaces and little Bloch type spaces.

MSC classification

Secondary: 47B38: Operators on function spaces (general) 30D45: Bloch functions, normal functions, normal families 46E15: Banach spaces of continuous, differentiable or analytic functions
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 69 , Issue 1 , August 2000 , pp. 41 - 60
Copyright
Copyright © Australian Mathematical Society 2000

References

[1]Bierstedt, K. D., Bonet, J. and Taskinen, J., ‘Associated weights and spaces of holomorphic functions’, Studia Math. 127 (1998), 137–168.CrossRefGoogle Scholar
[2]Bonet, J., Domański, P. and Lindström, M., ‘Essential norm and weak compactness of composition operator in wighted Banach spaces of analytic functions’, Canad. Math. Bull. 42 (1999), 139–148.Google Scholar
[3]Bonet, J., Domański, P., Lindström, M. and Taskinen, J., ‘Composition operators between weighted Banach spaces of analytic functions’, J. Austral. Math. Soc. (Ser. A) 64 (1998), 101–118.CrossRefGoogle Scholar
[4]Bourgain, J., ‘H ∞ is a Grothendieck space’, Studia Math. 75 (1983), 193–216.CrossRefGoogle Scholar
[5]Cima, J. A., ‘The basic properties of Bloch functions’, Internat. J. Math. and Math. Sci.. 2 (1979) 369–413.CrossRefGoogle Scholar
[6]Contreras, M. D. and Díaz-Madrigal, S., ‘Compact-type operators defined on H ∞’, Contemp. Math. 232 (1999), 111–118.CrossRefGoogle Scholar
[7]Cowen, C. and MacCluer, B., Composition operators on spaces of analytic functions (CRC Press, Boca Raton, 1995).Google Scholar
[8]Diestel, J., Sequences and series in Banach spaces (Springer, New York, 1984).Google Scholar
[9]Harman, P., Werner, D. and Werner, W., M-ideals in Banach spaces and Banach algebras, Lecture Notes in Math. 1547 (Springer, Berlin, 1993).CrossRefGoogle Scholar
[10]Hoffman, K., Banach spaces of analytic functions (Dover, New York, 1988).Google Scholar
[11]Jarchow, H., ‘Some functional analytic properties of composition operators’, Quaestiones Math. 18 (1995), 229–256.CrossRefGoogle Scholar
[12]jarchow, H. and Riedl, R., ‘Factorization fo composition operators through Bloch type spaces’, Illinois J. Math. 39 (1995), 431–440.CrossRefGoogle Scholar
[13]Liu, P., Saksman, E. and Tylli, H.-O., ‘Small composition operators on analytic vector-valued function spaces’, Spacific J. Math. 184 (1998), 295–309.Google Scholar
[14]Lusky, W., ‘On the structure of Hv0 (D) and hv0 (D)’, Math. Nachr. 159 (1992), 279–289.CrossRefGoogle Scholar
[15]Lusky, W., ‘On weighted spaces of harmonic and holomorphic functions’, J. London Math. Soc. (2) 51 (1995), 309–320.Google Scholar
[16]Madigan, K., ‘Composition operators on analytic Lipschtz spaces’, Proc. Amer. Math. soc.. 119 (1993), 465–473.CrossRefGoogle Scholar
[17]madigan, K. and Matheson, A., ‘Compact composition operators on the Bloch space’ Trans. Amer. Math. Soc. 347 (1995), 2679–2687.CrossRefGoogle Scholar
[18]Montes-Rodrfguez, A.. ‘The essential norm of a composition operator on Bloch spaces’, Pacific J. Math. 188 (1999), 339–351.Google Scholar
[19]Rubel, L. A. and Shield, A. L., ‘The second duals of certain spaces of analytic functions’, J. Austral. Math. Soc., 11 (1970), 276–280.CrossRefGoogle Scholar
[20]Shapiro, J. H., ‘The essential norm of a composition operator’, Ann. of Math. 125 (1987), 375–404.CrossRefGoogle Scholar
[21]Shapiro, J. H., ‘Compact composition operators on spaces of boundary-regular holomorphic functions’, Proc. Amer. Math. Soc. 100 (1987), 49–57.CrossRefGoogle Scholar
[22]Wojtaszczk, P., Banach spaces for analysts, Cambridge Stud. Adv. Math. 25 (Cambridge University Press, Cambridge, 1991).CrossRefGoogle Scholar
[23]Zhu, K., Operator theory in function spaces (Marcel Dekker, New York, 1990).Google Scholar
[24]Zhu, K., ‘Bloch type spaces of analytic functions’, Rocky Mountain J. Math. 23 (1993), 1143–1177.CrossRefGoogle Scholar