Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-24T00:28:57.940Z Has data issue: false hasContentIssue false
  • English
  • Français

Verma modules over Virasoro-like algebras

Part of: Lie algebras and Lie superalgebras

Published online by Cambridge University Press:  09 April 2009

Xian-Dong Wang  and
Kaiming Zhao
Xian-Dong Wang
Affiliation:
Department of Mathematics, Qingdao University, Qingdao 266071, P. R., China, e-mail: [email protected]
Kaiming Zhao
Affiliation:
Department of Mathematics, Wilfrid Laurier University, WaterlooOntario N2L 3C5, Canada, and Institute of Mathematics, Academy of Mathematics and System Sciences, Chinese Academy of Sciences, Beijing 100080, P. R., China, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

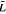Let K be a field of characteristic 0, G the direct sum of two copies of the additive group of integers. For a total order ≺ on G, which is compatible with the addition, and for any ċ1, ċ2 ∈ K, we define G-graded highest weight modules M(ċ1, ċ2, ≺) over the Virasoro-like algebra , indexed by G. It is natural to call them Verma modules. In the present paper, the irreducibility of M (ċ1, ċ2, ≺) is completely determined and the structure of reducible module M (ċ1, ċ2, ≺)is also described.

Keywords

Virasoro-like algebraVerma module.

MSC classification

Secondary: 17B10: Representations, algebraic theory (weights) 17B65: Infinite-dimensional Lie (super)algebras 17B68: Virasoro and related algebras
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 80 , Issue 2 , April 2006 , pp. 179 - 191
Copyright
Copyright © Australian Mathematical Society 2006

References

[1]Billin, Y. and Zhao, K., ‘Vertex operator representations of quantum tori at roots of unity’, Comm. Contemp. Math. 6 (2004), 195–220.CrossRefGoogle Scholar
[2]Djokovic, D. Z. and Zhao, K., ‘Some infinite-dimensional simple Lie algebras in characteristic 0 related to those of Blokc’, J. Pure Appl. Algebra 127 (1998), 153–165.CrossRefGoogle Scholar
[3]Rao, S. Eswara and Zhao, K., ‘Highest weight irrducible representations of rank 2 quantum tori’, Math. Res. Lett. 11 (2004), 615–628.CrossRefGoogle Scholar
[4]Gao, Y., ‘Representatoins of extended affine Lie algebras coordinatized by certain quantum tori’, Compositio Math. 123 (2000), 1–25.CrossRefGoogle Scholar
[5]Hu, J., Wang, X. and Zhao, K., ‘Verma modules over generalized Virasoro algebras Vir [G]’, J. Pure Appl. Algebra 177 (2003), 61–69.CrossRefGoogle Scholar
[6]Kac, V. G., Infinite dimensional Lie algebras (Cambridge University Press, 1990).CrossRefGoogle Scholar
[7]Kac, V. G. and Raina, K. A., Bombay lectures on highest weight representations of infinite dimensioal Lie algebras (World Sci., Singapore, 1987).Google Scholar
[8]Kirkman, E., Procesi, C. and Small, L. A., ‘q–analog for the Virasoro algebra’, Comm. Alg. 22 (1994), 3755–3774.CrossRefGoogle Scholar
[9]Mazorchuk, V., ‘Verma modules over generalized Witt algebras’, Compositio Math. 115 (1999), 21–35.CrossRefGoogle Scholar
[10]Moody, R. V. and Pianzola, A., Lie algebras with triangular decomposition (Wiley, New York, 1995).Google Scholar
[11]Zaytseva, M. I., ‘The set of orderings on abelian gorups’, Uspekhi Mat. Nauk 7 (1953), 135–137.Google Scholar
[12]Zhang, H. and Zhao, K., ‘Representations of the Virasoro-like algebra and its q–analog’, Comm. Alg. 24 (1996), 4361–4372.CrossRefGoogle Scholar
[13]Zhao, K., ‘Highest weight irreducible representations of the Virasora-like algebra’, preprint (2002).Google Scholar
[14]Zhao, K., ‘Weyl type algebras from quantum tori], to appear in Comm. Contemp. Math.Google Scholar