Hostname: page-component-745bb68f8f-b95js Total loading time: 0 Render date: 2025-01-11T06:26:17.125Z Has data issue: false hasContentIssue false
  • English
  • Français

VARIETIES GENERATED BY COMPLETELY 0-SIMPLE SEMIGROUPS

Part of: Semigroups Varieties

Published online by Cambridge University Press:  01 June 2008

NORMAN R. REILLY
NORMAN R. REILLY*
Affiliation:
Department of Mathematics, Simon Fraser University, 8888 University Drive, Burnaby, BC, Canada V5A 1S6 (email: [email protected])
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

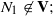Kublanovsky has shown that if a subvariety V of the variety RSn generated by completely 0-simple semigroups over groups of exponent n is itself generated by completely 0-simple semigroups, then it must satisfy one of three conditions: (i) A2 ∈ V; (ii) (iii) B2∈V but 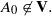The conditions (i) and (ii) are also sufficient conditions. In this note, we complete Kublanovsky’s programme by refining condition (iii) to obtain a complete set of conditions that are both necessary and sufficient.

Keywords

semigroupvarietyRees–Sushkevich varietiesexactcompletely 0-simple

MSC classification

Secondary: 20M07: Varieties and pseudovarieties of semigroups 08B15: Lattices of varieties
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 84 , Issue 3 , June 2008 , pp. 375 - 403
Copyright
Copyright © 2008 Australian Mathematical Society

References

[1]Graham, R. L., ‘On finite 0-simple semigroup and graph theory’, Math. Systems Theory 2 (1968), 325–339.Google Scholar
[2]Hall, T. E., Kublanovsky, S., Margolis, S., Sapir, M. and Trotter, P., ‘Algorithmic problems for finite groups and finite 0-simple semigroups’, J. Pure Appl. Algebra 119 (1997), 75–96.Google Scholar
[3]Howie, J. M., An Introduction to Semigroup Theory (Academic Press, London, 1976).Google Scholar
[4]Kublanovsky, S. I., On the Rees–Sushkevich variety, manuscript.Google Scholar
[5]Kublanovsky, S. I., Lee, E. W. H. and Reilly, N. R., ‘Sufficient conditions for the exactness of Rees–Sushkevich varieties’, Semigroup Forum 76 (2008), 87–94.Google Scholar
[6]Mashevitzky, G. I., ‘Identities in Brandt semigroups’, in: Semigroup Varieties and Semigroups of Endomorphisms, Collect. Sci. Works (Leningrad Gos. Ped. Inst., Leningrad, 1979), pp. 126–137 (in Russian).Google Scholar
[7]Mashevitzky, G. I., ‘Varieties generated by completely 0-simple semigroups’, in: Semigroups and Their Homomorphisms (ed. E. S. Lyapin) (Ross. Gos. Ped. Univ., Leningrad, 1991), pp. 53–62 (in Russian).Google Scholar
[8]Petrich, M. and Reilly, N. R., Completely Regular Semigroups (John Wiley and Sons, New York, 1999).Google Scholar
[9]Reilly, N. R., The interval [B2,NB2] in the lattice of Rees–Sushkevich varieties, Algebra Universalis, to appear.Google Scholar
[10]Reilly, N. R., ‘Complete congruences on the lattice of Rees–Sushkevich varieties’, Comm. Algebra 35 (2007), 3624–3659.CrossRefGoogle Scholar
[11]Trahtman, A. N., ‘A basis of identities of a five-element Brandt semigroup’, in: Issledovanija po Sovremennoj Algebre (Studies in Contemporary Algebra) (ed. L. N. Shevrin), Ural. Gos. Univ. Mat. Zap. 12, (3), 147–149, 1981 (in Russian) Sverdlovsk.Google Scholar
[12]Trahtman, A. N., ‘Identities of a five-element 0-simple semigroup’, Semigroup Forum 48 (1994), 385–387.Google Scholar
[13]Volkov, M. V., ‘On a question by Edmond W. H. Lee’, Izv. Ural. Gos. Univ. Mat. Mekh. 7(36) (2005), 167–178.Google Scholar