Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Wallis, Jennifer
1971.
A skew-Hadamard matrix of order 92.
Bulletin of the Australian Mathematical Society,
Vol. 5,
Issue. 2,
p.
203.
Wallis, Jennifer
1971.
Amicable hadamard matrices.
Journal of Combinatorial Theory, Series A,
Vol. 11,
Issue. 3,
p.
296.
Wallis, Jennifer
1972.
On integer matrices obeying certain matrix equations.
Journal of Combinatorial Theory, Series A,
Vol. 12,
Issue. 1,
p.
112.
Whittman, Albert Leon
1972.
Skew Hadamard matrices of Goethals-Seidel type.
Discrete Mathematics,
Vol. 2,
Issue. 4,
p.
397.
Wallis, Jennifer
1973.
Hadamard matrices of order 28m, 36m and 44m.
Journal of Combinatorial Theory, Series A,
Vol. 15,
Issue. 3,
p.
323.
Geramita, Anthony V.
and
Wallis, Jennifer Seberry
1976.
Combinatorial Mathematics IV.
Vol. 560,
Issue. ,
p.
46.
Koukouvinos, C.
and
Stylianou, S.
2008.
On skew-Hadamard matrices.
Discrete Mathematics,
Vol. 308,
Issue. 13,
p.
2723.
2020.
Hadamard Matrices.
p.
303.
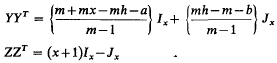 then
then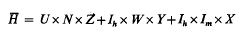 is an Hadamard matrix of order mxh.
is an Hadamard matrix of order mxh.