Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Tempesta, Piergiulio
2015.
The Lazard formal group, universal congruences and special values of zeta functions.
Transactions of the American Mathematical Society,
Vol. 367,
Issue. 10,
p.
7015.
Hu, Shuangnian
and
Zhao, Junyong
2017.
The Number of Rational Points of a Family of Algebraic Varieties over Finite Fields.
Algebra Colloquium,
Vol. 24,
Issue. 04,
p.
705.
Hu, Shuangnian
Qin, Xiaoer
and
Zhao, Junyong
2019.
Counting Rational Points of an Algebraic Variety over Finite Fields.
Results in Mathematics,
Vol. 74,
Issue. 1,
Zhao, Junyong
Zhao, Yang
and
Niu, Yujun
2020.
On the number of solutions of two-variable diagonal quartic equations over finite fields.
AIMS Mathematics,
Vol. 5,
Issue. 4,
p.
2979.
Komatsu, Takao
and
Zhu, Huilin
2020.
Hypergeometric Euler numbers.
AIMS Mathematics,
Vol. 5,
Issue. 2,
p.
1284.
Komatsu, Takao
and
Pandey, Ram Krishna
2021.
On hypergeometric Cauchy numbers of higher grade.
AIMS Mathematics,
Vol. 6,
Issue. 7,
p.
6630.
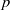 $p$ be a prime. In this paper, we present a detailed
$p$ be a prime. In this paper, we present a detailed 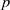 $p$-adic analysis on factorials and double factorials and their congruences. We give good bounds for the
$p$-adic analysis on factorials and double factorials and their congruences. We give good bounds for the 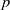 $p$-adic sizes of the coefficients of the divided universal Bernoulli number
$p$-adic sizes of the coefficients of the divided universal Bernoulli number 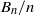 ${B}_{n} / n$ when
${B}_{n} / n$ when  $n$ is divisible by
$n$ is divisible by 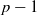 $p- 1$. Using these, we then establish the universal Kummer congruences modulo powers of a prime
$p- 1$. Using these, we then establish the universal Kummer congruences modulo powers of a prime 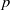 $p$ for the divided universal Bernoulli numbers
$p$ for the divided universal Bernoulli numbers 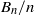 ${B}_{n} / n$ when
${B}_{n} / n$ when  $n$ is divisible by
$n$ is divisible by 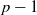 $p- 1$.
$p- 1$.