Published online by Cambridge University Press: 22 March 2017
Ott, Tomforde and Willis proposed a useful compactification for one-sided shifts over infinite alphabets. Building from their idea, we develop a notion of two-sided shift spaces over infinite alphabets, with an eye towards generalizing a result of Kitchens. As with the one-sided shifts over infinite alphabets, our shift spaces are compact Hausdorff spaces but, in contrast to the one-sided setting, our shift map is continuous everywhere. We show that many of the classical results from symbolic dynamics are still true for our two-sided shift spaces. In particular, while for one-sided shifts the problem about whether or not any 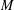 $M$-step shift is conjugate to an edge shift space is open, for two-sided shifts we can give a positive answer for this question.
$M$-step shift is conjugate to an edge shift space is open, for two-sided shifts we can give a positive answer for this question.
D. Gonçalves was partially supported by Capes grant PVE085/2012 and CNPq. M. Sobottka was supported by CNPq-Brazil grants 304813/2012-5, 480314/2013-6 and 308575/2015-6; part of this work was carried out while he was a postdoctoral fellow of CAPES-Brazil at the Center for Mathematical Modeling, University of Chile. C. Starling was supported by CNPq; work on this paper occurred while he held a postdoctoral fellowship at UFSC.