Published online by Cambridge University Press: 09 April 2009
The random processes discussed here may be specified in the following way. A fixed population of N members is spilt into two distinct classes. Individuals move about randomly between the classes, and we are interested in the size of each class at any time, rather than in the behaviour of particular individuals. Let i(t) and N —i(t) be the numbers present in the repective classes at the time t. It is assumed that the process {i(t), t ≧ 0} is Markovian, and that transitions between the states j = 0, 1, … N, occur according to the conditional probabilities;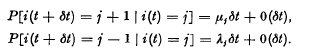 and
and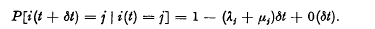 .
.