Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-26T13:02:59.507Z Has data issue: false hasContentIssue false
  • English
  • Français

Two estimates concerning asymptotics of the minimizations of a Ginzburg-Landau functional

Part of: Parabolic equations and systems Partial differential equations Elliptic equations and systems

Published online by Cambridge University Press:  09 April 2009

Min-Chun Hong
Min-Chun Hong
Affiliation:
Centre for Mathematics and its Applications The Australian National UniversityCanberra, ACT 0200, Australia
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove two asymptotical estimates for minimizers of a Ginzburg-Landau functional of the form .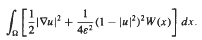

MSC classification

Secondary: 35B25: Singular perturbations 35J20: Variational methods for second-order elliptic equations 35K65: Degenerate parabolic equations
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 62 , Issue 1 , February 1997 , pp. 128 - 140
Copyright
Copyright © Australian Mathematical Society 1997

References

[1]Bethuel, F., Brezis, H. and Hélein, F., ‘Limite singuliere pour la minimisation de fonctionelles du type Ginzburg-Landau’, C.R. Acad. Sci. Paris Ser. I Math. 314 (1992), 891–895.Google Scholar
[2]Bethuel, F., Brezis, H. and Hélein, F., ‘Asympototics for the minimization of a Ginzburg-Landau functional’, Calc. Var. 1 (1993), 123–148.CrossRefGoogle Scholar
[3]Bethuel, F., Brezis, H. and Hélein, F., Ginzburg-Landau vortices (Birkhäuser, Basel, 1994).CrossRefGoogle Scholar
[4]Brezis, H., Merle, F. and Rivière, T., ‘Quantization effects for - Δu = u(1 − |u|2) in R 2’, Arch. Rational Mech. Anal. 126 (1994), 35–58.CrossRefGoogle Scholar
[5]Gilbarg, D. and Trudinger, N., Elliptic partial differential equations of second order, 2nd edition (Springer, Berlin, 1983).Google Scholar
[6]Hong, M.-C., ‘On a problem of Bethuel, Brezis and Helein concerning the Ginzburg-Landau functional’, C.R. Acad. Sci. Paris Ser. I Math. 320 (1995), 679–684.Google Scholar
[7]Lefter, C. and Radulescu, V. D., ‘On the Ginzburg-Landau energy with weight’, C.R. Acad. Sci. Paris Ser. I Math. (to appear).Google Scholar
[8]Struwe, M., ‘On the asymptotic behavior of minimizers of the Ginzburg-Landau model in 2 dimensions’, J. Differential Integral Equations 7 (1994), 1613–1624.Google Scholar
[9]Struwe, M., ‘An asymptotic estimate for the Ginzburg-Landau model’, C. R. Acad. Sci. Paris Ser. I Math. 317 (1993), 677–680.Google Scholar
[10]Struwe, M., Singular perturbations of geometric variational problems (to appear) (University of Minnesota, Mineapolis, 1994).Google Scholar
[11]Struwe, M., private communication.Google Scholar