Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Davey, Brian A.
and
Haviar, Miroslav
2004.
Applications of Priestley duality in transferring optimal dualities.
Studia Logica,
Vol. 78,
Issue. 1-2,
p.
213.
Gouveia, Maria Joao
and
Haviar, Miroslav
2011.
Transferral of entailment in duality theory: Dualisability.
Czechoslovak Mathematical Journal,
Vol. 61,
Issue. 1,
p.
41.
Solovyov, Sergey A.
2014.
Variable-basis Categorically-algebraic Dualities.
Fuzzy Information and Engineering,
Vol. 6,
Issue. 4,
p.
393.


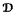 generated by a finite algebra
generated by a finite algebra 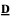 and assume that
and assume that 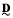 yields a natural duality on
yields a natural duality on 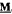 , which is also optimal modulo endormorphisms, for any finite algebra
, which is also optimal modulo endormorphisms, for any finite algebra 