Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-23T19:50:57.219Z Has data issue: false hasContentIssue false
  • English
  • Français

TRACES ARISING FROM REGULAR INCLUSIONS

Part of: Selfadjoint operator algebras

Published online by Cambridge University Press:  03 November 2016

DANNY CRYTSER  and
GABRIEL NAGY
DANNY CRYTSER*
Affiliation:
Department of Mathematics, Kansas State University, Manhattan, KS 66503, USA email [email protected]
GABRIEL NAGY
Affiliation:
Department of Mathematics, Kansas State University, Manhattan, KS 66503, USA email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study the problem of extending a state on an abelian 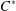$C^{\ast }$-subalgebra to a tracial state on the ambient 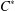$C^{\ast }$-algebra. We propose an approach that is well suited to the case of regular inclusions, in which there is a large supply of normalizers of the subalgebra. Conditional expectations onto the subalgebra give natural extensions of a state to the ambient 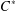$C^{\ast }$-algebra; we prove that these extensions are tracial states if and only if certain invariance properties of both the state and conditional expectations are satisfied. In the example of a groupoid 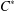$C^{\ast }$-algebra, these invariance properties correspond to invariance of associated measures on the unit space under the action of bisections. Using our framework, we are able to completely describe the tracial state space of a Cuntz–Krieger graph algebra. Along the way we introduce certain operations called graph tightenings, which both streamline our description and provide connections to related finiteness questions in graph 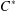$C^{\ast }$-algebras. Our investigation has close connections with the so-called unique state extension property and its variants.

Keywords

operator algebrastracial statesC∗ -algebrasgraph algebras

MSC classification

Primary: 46L30: States
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 103 , Issue 2 , October 2017 , pp. 190 - 230
Copyright
© 2016 Australian Mathematical Publishing Association Inc. 

References

Archbold, R. J., Bunce, J. W. and Gregson, K. D., ‘Extensions of states of C ∗ -algebras, II’, Proc. Edinb. Math. Soc. 92A (1982), 113–122.Google Scholar
Brown, J., Nagy, G. and Reznikoff, S., ‘A generalized Cuntz–Krieger uniqueness theorem for higher-rank graphs’, J. Funct. Anal. 266(4) (2013), 2590–2609.Google Scholar
Brown, J., Nagy, G., Reznikoff, S., Sims, A. and Williams, D., ‘Cartan subalgebras in C ∗ -algebras of Hausdorff etale groupoids’, Integral Equations Operator Theory 85(1) (2016), 109–126.CrossRefGoogle Scholar
Cuntz, J. and Pedersen, G. K., ‘Equivalence and traces on C ∗ -algebras’, J. Funct. Anal. 33(2) (1979), 135–164.Google Scholar
Elliott, G. and Toms, A., ‘Regularity properties in the classification program for separable amenable C ∗ -algebras’, Bull. Amer. Math. Soc. 45 (2008), 229–245.Google Scholar
Feldman, J. and Moore, C. C., ‘Ergodic equivalence relations, cohomology, and von Neumann algebras. II’, Trans. Amer. Math. Soc. 234(2) (1977), 325–359.Google Scholar
Goehle, G., ‘Groupoid C ∗ -algebras with Hausdorff spectrum’, Bull. Aust. Math. Soc. 88(2) (2013), 232–242.CrossRefGoogle Scholar
Hjelmborg, J., ‘Purely infinite and stable C ∗ -algebras of graphs and dynamical systems’, Ergodic Theory Dynam. Systems 21(6) (2001), 1789–1808.Google Scholar
an Huef, A. and Raeburn, I., ‘The ideal structure of Cuntz–Krieger algebras’, Ergodic Theory Dynam. Systems 17(3) (1997), 611–624.Google Scholar
Jeong, J., Park, G. and Shin, D., ‘Stable rank and real rank of graph C ∗ -algebras’, Pacific J. Math. 200(2) (2001), 331–343.Google Scholar
Johnson, M., ‘The graph traces of finite graphs and applications to tracial states of C ∗ -algebras’, New York J. Math. 11 (2005), 649–658.Google Scholar
Kadison, R. and Singer, I., ‘Extensions of pure states’, Amer. J. Math. 81(2) (1960), 383–400.Google Scholar
Kumjian, A., ‘On C ∗ -diagonals’, Canad. J. Math. 38(4) (1986), 969–1008.Google Scholar
Kumjian, A., Pask, D., Raeburn, I. and Renault, J., ‘Graphs, groupoids, and Cuntz–Krieger algebras’, J. Funct. Anal. 144(2) (1997), 505–541.Google Scholar
Lance, E. C., Hilbert C ∗ -Modules: A Toolkit for Operator Algebraists, London Mathematical Society Lecture Note Series, 210 (Cambridge University Press, 1994).Google Scholar
Nagy, G. and Reznikoff, S., ‘Abelian core of graph algebras’, J. Lond. Math. Soc. 85(3) (2012), 889–908.Google Scholar
Nagy, G. and Reznikoff, S., ‘Pseudo-diagonals and uniqueness theorems’, Proc. Amer. Math. Soc. 142(1) (2014), 263–275.Google Scholar
Pask, D. and Rennie, A., ‘The noncommutative geometry of graph C ∗ -algebras I: the index theorem’, J. Funct. Anal. 233(1) (2006), 92–134.Google Scholar
Pedersen, G.K., C ∗ -Algebras and their Automorphism Groups (Academic Press, 1979).Google Scholar
Pitts, D., ‘Structure for regular inclusions’, Preprint, 2012, arXiv:1202.6413.Google Scholar
Powers, R., ‘Simplicity of the C ∗ -algebra associated with the free group on two generators’, Duke Math. J. 42(1) (1975), 151–156.Google Scholar
Raeburn, I., Graph Algebras, CBMS Lecture Notes (American Mathematical Society, 2005).Google Scholar
Renault, J., A Groupoid Approach to C ∗ -Algebras, Lecture Notes in Mathematics (Springer, 1980).CrossRefGoogle Scholar
Renault, J., ‘Cartan subalgebras in C ∗ -algebras’, Irish Math. Soc. Bull. 61 (2008), 29–63.Google Scholar
Rieffel, M., ‘ C ∗ -algebras associated to irrational rotations’, Pacific J. Math. 93(2) (1981), 415–429.CrossRefGoogle Scholar
Schafhauser, C., ‘AF-embeddings of graph algebras’, Preprint, 2014, arXiv:1405.7757.Google Scholar
Schafhauser, C., ‘Traces on topological graph algebras’, Preprint, 2016, arXiv:1605.03603.Google Scholar
Tomforde, M., ‘The ordered K 0 -group of a graph C ∗ -algebra’, C. R. Math. Acad. Sci. Soc. R. Can. 25 (2003), 19–25.Google Scholar
Tomforde, M., ‘A unified approach to Exel–Laca algebras and C ∗ -algebras associated to graphs’, J. Operator Theory 50 (2003), 345–368.Google Scholar
Tomforde, M., ‘Stability of C ∗ -algebras affiliated to graphs’, Proc. Amer. Math. Soc. 132(6) (2004), 1787–1795.CrossRefGoogle Scholar
Winter, W. and Zacharias, J., ‘The nuclear dimension of C ∗ -algebras’, Adv. Math. 224(1) (2010), 461–498.Google Scholar