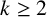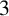1 Introduction
The
![]() $3$
-strand braid group has many interesting quotients admitting realizations as reflection groups of rank two over
$3$
-strand braid group has many interesting quotients admitting realizations as reflection groups of rank two over
![]() $\mathbb {R}$
or
$\mathbb {R}$
or
![]() $\mathbb {C}$
, the most famous one being the symmetric group
$\mathbb {C}$
, the most famous one being the symmetric group
![]() $\mathfrak {S}_3$
. The symmetric group
$\mathfrak {S}_3$
. The symmetric group
![]() $\mathfrak {S}_3$
is a finite real reflection group or finite Coxeter group, and the
$\mathfrak {S}_3$
is a finite real reflection group or finite Coxeter group, and the
![]() $3$
-strand braid group is isomorphic to the corresponding Artin–Tits group. In this case, the quotient map from
$3$
-strand braid group is isomorphic to the corresponding Artin–Tits group. In this case, the quotient map from
![]() $\mathcal {B}_3$
to
$\mathcal {B}_3$
to
![]() $\mathfrak {S}_3$
maps Dehn twists to reflections. This situation admits a well-known generalization, where the symmetric group is replaced by any (not necessarily finite) Coxeter group and the braid group by the corresponding Artin–Tits group (see for instance [Reference Kassel and Turaev21, Section 6.6] for an introduction to the topic). In this situation, one has a natural recipe to attach to a Coxeter group a group playing the role of the braid group and sharing the same kind of (in general, conjectural) properties—absence of torsion, solvable word and conjugacy problems, and so forth.
$\mathfrak {S}_3$
maps Dehn twists to reflections. This situation admits a well-known generalization, where the symmetric group is replaced by any (not necessarily finite) Coxeter group and the braid group by the corresponding Artin–Tits group (see for instance [Reference Kassel and Turaev21, Section 6.6] for an introduction to the topic). In this situation, one has a natural recipe to attach to a Coxeter group a group playing the role of the braid group and sharing the same kind of (in general, conjectural) properties—absence of torsion, solvable word and conjugacy problems, and so forth.
In the complex case, that is, if we start with a finite complex reflection group, there is also a way to attach a group with the same kind of properties as the braid group: one defines the braid group attached to a finite complex reflection group as the fundamental group of the space of regular orbits in the natural representation of the reflection group [Reference Broué, Malle and Rouquier12]. This allows one to recover the
![]() $3$
-strand braid group from several finite complex reflection groups of rank two arising as quotients—like for instance
$3$
-strand braid group from several finite complex reflection groups of rank two arising as quotients—like for instance
![]() $G_4$
in Shephard–Todd notation. In the cases where the reflection group can be realized over the real numbers, that is, in the cases where it is a finite Coxeter group, the obtained braid group is isomorphic to the Artin–Tits group of the Coxeter group [Reference Brieskorn9]. In the complex case, the generalizations of Dehn twists are given by so-called braided reflections, which are also mapped to reflections in the quotients.
$G_4$
in Shephard–Todd notation. In the cases where the reflection group can be realized over the real numbers, that is, in the cases where it is a finite Coxeter group, the obtained braid group is isomorphic to the Artin–Tits group of the Coxeter group [Reference Brieskorn9]. In the complex case, the generalizations of Dehn twists are given by so-called braided reflections, which are also mapped to reflections in the quotients.
In this paper, we study another kind of generalization of reflection quotients of the
![]() $3$
-strand braid group. A feature of the
$3$
-strand braid group. A feature of the
![]() $3$
-strand braid group is that it is isomorphic to the knot group of the trefoil knot [Reference Kassel and Turaev21, Section 1.1.4], which is a torus knot (that is, a knot that lies on the surface of a torus). Several finite complex reflection groups with a single conjugacy class of reflecting hyperplanes have their braid group isomorphic to a torus knot group [Reference Bannai5], and the quotient map from the torus knot group to the complex reflection group maps meridians—which one can consider as generalizations of Dehn twists—to reflections. Moreover, as in the aforementioned cases, a presentation of the reflection group is obtained from a presentation of the torus knot group having meridians as generators by setting
$3$
-strand braid group is that it is isomorphic to the knot group of the trefoil knot [Reference Kassel and Turaev21, Section 1.1.4], which is a torus knot (that is, a knot that lies on the surface of a torus). Several finite complex reflection groups with a single conjugacy class of reflecting hyperplanes have their braid group isomorphic to a torus knot group [Reference Bannai5], and the quotient map from the torus knot group to the complex reflection group maps meridians—which one can consider as generalizations of Dehn twists—to reflections. Moreover, as in the aforementioned cases, a presentation of the reflection group is obtained from a presentation of the torus knot group having meridians as generators by setting
![]() $x^k=1$
for some
$x^k=1$
for some
![]() $k\geq 2$
for any (equivalently every) meridian x. The obtained reflection groups—which include the aforementioned quotients of the
$k\geq 2$
for any (equivalently every) meridian x. The obtained reflection groups—which include the aforementioned quotients of the
![]() $3$
-strand braid group—are of rank two, that is, they are reflection groups over
$3$
-strand braid group—are of rank two, that is, they are reflection groups over
![]() $\mathbb {C}^2$
. The aim of this paper is to study all possible quotients of all possible torus knot groups arising in this way. Note that surjective maps from link groups onto Coxeter or reflection groups, which have the property that they send meridians to reflections, arise in a knot-theoretic setting in the study of the so-called meridional rank conjecture stating an equality between the bridge number of a link L and its meridional rank (see [Reference Baader, Blair and Kjuchukova3, Reference Baader, Blair, Kjuchukova and Misev4]). Indeed, if one finds such a surjective map from
$\mathbb {C}^2$
. The aim of this paper is to study all possible quotients of all possible torus knot groups arising in this way. Note that surjective maps from link groups onto Coxeter or reflection groups, which have the property that they send meridians to reflections, arise in a knot-theoretic setting in the study of the so-called meridional rank conjecture stating an equality between the bridge number of a link L and its meridional rank (see [Reference Baader, Blair and Kjuchukova3, Reference Baader, Blair, Kjuchukova and Misev4]). Indeed, if one finds such a surjective map from
![]() $\Gamma =\pi _1(S^3\backslash L)$
onto W, where L is a link and W a reflection group, then the meridian rank of L, that is, the minimal number of meridians needed to generate
$\Gamma =\pi _1(S^3\backslash L)$
onto W, where L is a link and W a reflection group, then the meridian rank of L, that is, the minimal number of meridians needed to generate
![]() $\Gamma $
, is necessarily bounded below by the reflection rank of W, that is, the minimal number of reflections needed to generate W. This conjecture is solved for torus links [Reference Rost and Zieschang30].
$\Gamma $
, is necessarily bounded below by the reflection rank of W, that is, the minimal number of reflections needed to generate W. This conjecture is solved for torus links [Reference Rost and Zieschang30].
The aforementioned quotients of torus knot groups studied in this paper are infinite in general. We show that they are generalizations of complex reflection groups of rank two, with the torus knot group playing the role of an attached ‘braid group’, and give a few fundamental results on their structure as well as a classification.
To be more precise, let
![]() $n,m\geq 2$
be two relatively prime integers, with
$n,m\geq 2$
be two relatively prime integers, with
![]() $n<m$
. The torus knot group
$n<m$
. The torus knot group
![]() $G(n,m)$
is the fundamental group of the complement of the torus knot
$G(n,m)$
is the fundamental group of the complement of the torus knot
![]() $T_{n,m}$
in
$T_{n,m}$
in
![]() $\mathbb {R}^3$
. It admits (see for instance [Reference Rolfsen29, Ch. 3, Section C]) the well-known presentation
$\mathbb {R}^3$
. It admits (see for instance [Reference Rolfsen29, Ch. 3, Section C]) the well-known presentation
Another presentation, which we call classical, is given by
where indices are taken modulo n. See for instance [Reference Bessis6, 6.4, Problem 10]. An explicit isomorphism between
![]() $G(n,m)$
and the group with Presentation (1-2) is given by
$G(n,m)$
and the group with Presentation (1-2) is given by
![]() $x\mapsto x_1 x_2 \cdots x_m$
,
$x\mapsto x_1 x_2 \cdots x_m$
,
![]() $y\mapsto x_1 x_2 \cdots x_n$
. Note that in Presentation (1-2), the generators are meridians. To see this, one can for instance use [Reference Burde, Zieschang and Heusener13, Proposition 3.38(b)], where it is shown that if
$y\mapsto x_1 x_2 \cdots x_n$
. Note that in Presentation (1-2), the generators are meridians. To see this, one can for instance use [Reference Burde, Zieschang and Heusener13, Proposition 3.38(b)], where it is shown that if
![]() $a,b\in \mathbb {Z}$
are such that
$a,b\in \mathbb {Z}$
are such that
![]() $an-bm=1$
, then
$an-bm=1$
, then
![]() $y^a x^{-b}$
is a meridian. Using the defining relations of Presentation (1-2), we see that under the isomorphism given above, the element
$y^a x^{-b}$
is a meridian. Using the defining relations of Presentation (1-2), we see that under the isomorphism given above, the element
![]() $y^a x^{-b}$
is mapped to
$y^a x^{-b}$
is mapped to
![]() $x_i^{\pm 1}$
for some i, and hence there is an i such that
$x_i^{\pm 1}$
for some i, and hence there is an i such that
![]() $x_i$
is a meridian. However, since n and m are coprime, all
$x_i$
is a meridian. However, since n and m are coprime, all
![]() $x_i$
are conjugate, and hence they are all meridians. Using the fact that the torus knots
$x_i$
are conjugate, and hence they are all meridians. Using the fact that the torus knots
![]() $T_{n,m}$
and
$T_{n,m}$
and
![]() $T_{m,n}$
are isotopic, one obtains a third presentation, where generators are also meridians, which we call dual, given by
$T_{m,n}$
are isotopic, one obtains a third presentation, where generators are also meridians, which we call dual, given by
In the case where
![]() $n=2$
,
$n=2$
,
![]() $m=3$
(more generally, for m odd), the classical presentation above is the classical presentation of the
$m=3$
(more generally, for m odd), the classical presentation above is the classical presentation of the
![]() $3$
-strand braid group
$3$
-strand braid group
![]() $\mathcal {B}_3$
(more generally, of the Artin–Tits group of dihedral type
$\mathcal {B}_3$
(more generally, of the Artin–Tits group of dihedral type
![]() $I_2(m)$
), while the dual presentation is Birman, Ko, and Lee’s presentation [Reference Birman, Ko and Lee7] (more generally, the dual presentation in the sense of [Reference Bessis6]). This explains our terminology. Presentation (1-1) is obtained from the classical one by setting
$I_2(m)$
), while the dual presentation is Birman, Ko, and Lee’s presentation [Reference Birman, Ko and Lee7] (more generally, the dual presentation in the sense of [Reference Bessis6]). This explains our terminology. Presentation (1-1) is obtained from the classical one by setting
![]() $x=x_1 x_2 x_1$
,
$x=x_1 x_2 x_1$
,
![]() $y=x_1 x_2$
, while the third one is obtained by setting
$y=x_1 x_2$
, while the third one is obtained by setting
![]() $y_1=x_1$
,
$y_1=x_1$
,
![]() $y_2=x_2$
,
$y_2=x_2$
,
![]() $y_3=x_1 x_2 x_1^{-1}$
. The symmetric group
$y_3=x_1 x_2 x_1^{-1}$
. The symmetric group
![]() $\mathfrak {S}_3$
is obtained from either the classical or dual presentation by adding the relations
$\mathfrak {S}_3$
is obtained from either the classical or dual presentation by adding the relations
![]() $a^2=1$
for all generators a (or for a single generator a, as they are all conjugate). The complex reflection groups mentioned above are obtained in a similar way by setting
$a^2=1$
for all generators a (or for a single generator a, as they are all conjugate). The complex reflection groups mentioned above are obtained in a similar way by setting
![]() $a^k=1$
for the generators a and some
$a^k=1$
for the generators a and some
![]() $k\geq 2$
, and the images of the generators (and more generally, the meridians) in the quotient are reflections. More precisely, in Shephard–Todd notation:
$k\geq 2$
, and the images of the generators (and more generally, the meridians) in the quotient are reflections. More precisely, in Shephard–Todd notation:
-
•
 $G_4$
,
$G_4$
,
 $G_8$
, and
$G_8$
, and
 $G_{16}$
are obtained from the classical presentation of
$G_{16}$
are obtained from the classical presentation of
 $\mathcal {B}_3\cong G(2,3)$
by adding the relations
$\mathcal {B}_3\cong G(2,3)$
by adding the relations
 $x_i^k=1$
for all i, where
$x_i^k=1$
for all i, where
 $k=3, 4$
, and
$k=3, 4$
, and
 $5$
, respectively;
$5$
, respectively; -
•
 $G_{12}$
is obtained from the classical presentation of
$G_{12}$
is obtained from the classical presentation of
 $G(3,4)$
by adding the relations
$G(3,4)$
by adding the relations
 $x_i^2=1$
for all i;
$x_i^2=1$
for all i; -
•
 $G_{22}$
is obtained from the classical presentation of
$G_{22}$
is obtained from the classical presentation of
 $G(3,5)$
by adding the relations
$G(3,5)$
by adding the relations
 $x_i^2=1$
for all i;
$x_i^2=1$
for all i; -
•
 $G_{20}$
is obtained from the classical presentation of
$G_{20}$
is obtained from the classical presentation of
 $G(2,5)$
by adding the relation
$G(2,5)$
by adding the relation
 $x_i^3=1$
for all i;
$x_i^3=1$
for all i; -
• for odd m, the group
 $G(m,m,2)$
, which is also the dihedral Coxeter group of type
$G(m,m,2)$
, which is also the dihedral Coxeter group of type
 $I_2(m)$
, is obtained from
$I_2(m)$
, is obtained from
 $G(2,m)$
by adding the relation
$G(2,m)$
by adding the relation
 $x_i^2=1$
for all i. Note that in this case,
$x_i^2=1$
for all i. Note that in this case,
 $G(2,m)$
is the Artin–Tits group of type
$G(2,m)$
is the Artin–Tits group of type
 $I_2(m)$
.
$I_2(m)$
.
Generalizing the groups obtained in the first point above, Coxeter [Reference Coxeter15] studied the quotient of
![]() $\mathcal {B}_3$
(and more generally,
$\mathcal {B}_3$
(and more generally,
![]() $\mathcal {B}_n$
) by the relations
$\mathcal {B}_n$
) by the relations
![]() $x_1^k=x_2^k=1$
, where
$x_1^k=x_2^k=1$
, where
![]() $k\geq 2$
, and showed that this quotient is finite if and only if
$k\geq 2$
, and showed that this quotient is finite if and only if
![]() $k\leq 5$
. He also showed that these groups, which are sometimes called truncated braid groups, admit a complex representation as groups generated by (pseudo-)reflections. For
$k\leq 5$
. He also showed that these groups, which are sometimes called truncated braid groups, admit a complex representation as groups generated by (pseudo-)reflections. For
![]() $k\leq 5$
, he showed that this representation is faithful, and that the group is finite if and only if
$k\leq 5$
, he showed that this representation is faithful, and that the group is finite if and only if
![]() $k\leq 5$
.
$k\leq 5$
.
Let
![]() $n,m$
be as above and
$n,m$
be as above and
![]() $k\geq 2$
. We define a three-parameter family of groups generalizing all the examples given above, called toric reflection groups, by setting
$k\geq 2$
. We define a three-parameter family of groups generalizing all the examples given above, called toric reflection groups, by setting
 $$ \begin{align}W(k,n,m):=\left\langle x_1, x_2, \ldots, x_n \ \vert\ \begin{matrix} x_i^k=1~\text{for}~i=1, \ldots, n,\\ \underbrace{x_1 x_2 \cdots}_{m~\text{factors}} = \underbrace{x_2 x_3\cdots}_{m~\text{factors}} = \cdots = \underbrace{x_n x_1 \cdots}_{m~\text{factors}} \end{matrix} \right\rangle.\end{align} $$
$$ \begin{align}W(k,n,m):=\left\langle x_1, x_2, \ldots, x_n \ \vert\ \begin{matrix} x_i^k=1~\text{for}~i=1, \ldots, n,\\ \underbrace{x_1 x_2 \cdots}_{m~\text{factors}} = \underbrace{x_2 x_3\cdots}_{m~\text{factors}} = \cdots = \underbrace{x_n x_1 \cdots}_{m~\text{factors}} \end{matrix} \right\rangle.\end{align} $$
We define the conjugates of the nontrivial powers
![]() $x_i^\ell $
(that is, not equal to the identity) of the generators
$x_i^\ell $
(that is, not equal to the identity) of the generators
![]() $x_i$
to be the reflections in
$x_i$
to be the reflections in
![]() $W(k,n,m)$
. This is partly justified by the fact that in the aforementioned cases where
$W(k,n,m)$
. This is partly justified by the fact that in the aforementioned cases where
![]() $W(k,n,m)$
is finite, the
$W(k,n,m)$
is finite, the
![]() $x_i$
are reflections, and more generally, by the following fact. We show in Theorem 1.1 that these groups are isomorphic to groups that are part of a family of groups introduced by Achar and Aubert, called J-groups [Reference Achar and Aubert2], which are generalizations of complex reflection groups of rank two—see Section 2.1 for precise definitions, and Theorem 2.12 together with Corollary 2.13 for a more precise and complete statement. Each such group admits a representation as a subgroup of
$x_i$
are reflections, and more generally, by the following fact. We show in Theorem 1.1 that these groups are isomorphic to groups that are part of a family of groups introduced by Achar and Aubert, called J-groups [Reference Achar and Aubert2], which are generalizations of complex reflection groups of rank two—see Section 2.1 for precise definitions, and Theorem 2.12 together with Corollary 2.13 for a more precise and complete statement. Each such group admits a representation as a subgroup of
![]() $\mathrm {GL}_2(\mathbb {C})$
generated by (pseudo-)reflections [Reference Achar and Aubert2, Section 4]. Achar and Aubert showed that a J-group is finite if and only if it is a finite complex reflection group of rank two [Reference Achar and Aubert2, Theorem 1.2].
$\mathrm {GL}_2(\mathbb {C})$
generated by (pseudo-)reflections [Reference Achar and Aubert2, Section 4]. Achar and Aubert showed that a J-group is finite if and only if it is a finite complex reflection group of rank two [Reference Achar and Aubert2, Theorem 1.2].
Theorem 1.1 (Toric reflection groups are J-groups)
The group
![]() $W(k,n,m)$
is isomorphic to the J-group
$W(k,n,m)$
is isomorphic to the J-group
![]() $J(\begin {smallmatrix} k & n & m \\ & n & m \end {smallmatrix})$
of Achar and Aubert. Under this isomorphism, the generators of
$J(\begin {smallmatrix} k & n & m \\ & n & m \end {smallmatrix})$
of Achar and Aubert. Under this isomorphism, the generators of
![]() $W(k,n,m)$
correspond to elements of the J-group acting by reflections in Achar and Aubert’s representation.
$W(k,n,m)$
correspond to elements of the J-group acting by reflections in Achar and Aubert’s representation.
This allows one to consider Presentation (1-3) as a presentation of a reflection group in some sense. Nevertheless, let us point out that Achar and Aubert’s representation is not faithful in general: see Section 2.3. We say that two toric reflection groups
![]() $W(k,n,m)$
,
$W(k,n,m)$
,
![]() $W(k',n',m')$
with respective sets of reflections
$W(k',n',m')$
with respective sets of reflections
![]() $R, R'$
are reflection isomorphic, written
$R, R'$
are reflection isomorphic, written
![]() $W(k,n,m)\cong _{\mathrm {ref}}W(k',n',m')$
, if there is a group isomorphism
$W(k,n,m)\cong _{\mathrm {ref}}W(k',n',m')$
, if there is a group isomorphism
![]() $\varphi : W(k,n,m)\longrightarrow W(k',n',m')$
such that
$\varphi : W(k,n,m)\longrightarrow W(k',n',m')$
such that
![]() $\varphi (R)=R'$
. The following statement classifies toric reflection groups (see Theorem 4.1 below).
$\varphi (R)=R'$
. The following statement classifies toric reflection groups (see Theorem 4.1 below).
Theorem 1.2 (Classification of toric reflection groups)
Let
![]() $k,k',n,n',m,m'\geq 2$
with
$k,k',n,n',m,m'\geq 2$
with
![]() $n<m$
,
$n<m$
,
![]() $n'<m'$
, n and m coprime, and
$n'<m'$
, n and m coprime, and
![]() $n'$
and
$n'$
and
![]() $m'$
coprime. Then,
$m'$
coprime. Then,
Note that Presentation (1-3) can be given as well if
![]() $n>m$
. However, in this case, thanks to the isomorphism
$n>m$
. However, in this case, thanks to the isomorphism
![]() $G(n,m)\cong G(m,n)$
and the fact that the toric reflection group is obtained from the torus knot group by killing the k th power of meridians, we get that
$G(n,m)\cong G(m,n)$
and the fact that the toric reflection group is obtained from the torus knot group by killing the k th power of meridians, we get that
![]() $W(k,n,m)\cong W(k,m,n)$
. Hence, the case
$W(k,n,m)\cong W(k,m,n)$
. Hence, the case
![]() $n<m$
is sufficient to parameterize all toric reflection groups, and with this assumption, Theorem 1.2 says that for any toric reflection group W, there is a single pair
$n<m$
is sufficient to parameterize all toric reflection groups, and with this assumption, Theorem 1.2 says that for any toric reflection group W, there is a single pair
![]() $(k,n,m)$
with
$(k,n,m)$
with
![]() $W\cong _{\mathrm {ref}} W(k,n,m)$
.
$W\cong _{\mathrm {ref}} W(k,n,m)$
.
As an immediate corollary of Theorem 1.2, we get the following definition of the braid group of a toric reflection group, in the spirit of Achar and Aubert’s characterization of finite J-groups. Given a toric reflection group W, let
![]() $k,n,m\geq 2$
with
$k,n,m\geq 2$
with
![]() $n<m$
and
$n<m$
and
![]() $n,m$
coprime such that
$n,m$
coprime such that
![]() $W\cong _{\mathrm {ref}} W(k,n,m)$
. We set
$W\cong _{\mathrm {ref}} W(k,n,m)$
. We set
![]() $\mathcal {B}(W,R):=G(n,m)$
.
$\mathcal {B}(W,R):=G(n,m)$
.
Corollary 1.3 (Braid groups of toric reflection groups)
Let W be a toric reflection group with set of reflections R. Then we have the following.
-
(1) The group
 $\mathcal {B}(W,R)$
is well defined, that is, only depends on the isomorphism class of the toric reflection group of W.
$\mathcal {B}(W,R)$
is well defined, that is, only depends on the isomorphism class of the toric reflection group of W. -
(2) If W is finite, then
 $\mathcal {B}(W,R)$
is isomorphic to the braid group of the complex reflection group W.
$\mathcal {B}(W,R)$
is isomorphic to the braid group of the complex reflection group W.
Note that Schreier [Reference Schreier31] proved that two torus knot groups
![]() $G(n,m)$
and
$G(n,m)$
and
![]() $G(n',m')$
(
$G(n',m')$
(
![]() ${n<m}$
and
${n<m}$
and
![]() $n'<m'$
) are isomorphic (as abstract groups) if and only if
$n'<m'$
) are isomorphic (as abstract groups) if and only if
![]() $n=n'$
and
$n=n'$
and
![]() $m=m'$
(his result is actually more general as he did not assume the parameters to be coprime).
$m=m'$
(his result is actually more general as he did not assume the parameters to be coprime).
The above corollary yields the generalization of reflection quotients of the
![]() $3$
-strand braid group announced at the beginning of the introduction. Note that every torus knot group is a Garside group [Reference Dehornoy and Paris17, Example 4] (see also [Reference Gobet20, Section 3] and [Reference Dehornoy, Digne, Krammer, Godelle and Michel16] for basics on Garside groups), and hence it shares many properties with Artin’s braid groups and more generally Artin–Tits groups of spherical type, that is, attached to finite Coxeter groups, which are all Garside groups. Such groups have, for instance, solvable word and conjugacy problems, and are torsion-free. Note that Artin–Tits groups attached to infinite Coxeter groups are not Garside groups in general (some of them are known to be so-called quasi-Garside groups [Reference Dehornoy, Digne, Krammer, Godelle and Michel16]), while by Corollary 1.3, an infinite toric reflection group has an attached ‘braid group’ which is always a Garside group. This is not especially surprising and could already be observed for Coxeter’s truncated braid groups [Reference Coxeter15], as toric reflection groups have, even when infinite, properties similar to finite (irreducible) Coxeter groups. For instance, they have a nontrivial cyclic center—see Corollary 1.6.
$3$
-strand braid group announced at the beginning of the introduction. Note that every torus knot group is a Garside group [Reference Dehornoy and Paris17, Example 4] (see also [Reference Gobet20, Section 3] and [Reference Dehornoy, Digne, Krammer, Godelle and Michel16] for basics on Garside groups), and hence it shares many properties with Artin’s braid groups and more generally Artin–Tits groups of spherical type, that is, attached to finite Coxeter groups, which are all Garside groups. Such groups have, for instance, solvable word and conjugacy problems, and are torsion-free. Note that Artin–Tits groups attached to infinite Coxeter groups are not Garside groups in general (some of them are known to be so-called quasi-Garside groups [Reference Dehornoy, Digne, Krammer, Godelle and Michel16]), while by Corollary 1.3, an infinite toric reflection group has an attached ‘braid group’ which is always a Garside group. This is not especially surprising and could already be observed for Coxeter’s truncated braid groups [Reference Coxeter15], as toric reflection groups have, even when infinite, properties similar to finite (irreducible) Coxeter groups. For instance, they have a nontrivial cyclic center—see Corollary 1.6.
A main ingredient in the proof of Theorem 1.2 is the theory of Coxeter groups and their parabolic subgroups, especially in rank three. In the following, we show several results which are purely Coxeter-theoretic, and might be of independent interest. To establish Theorem 1.2, we identify the quotient of a toric reflection group W by its center. More precisely, let
![]() $k,n,m$
be as above, and let
$k,n,m$
be as above, and let
![]() $W_{k,n,m}$
be the rank-three Coxeter group
$W_{k,n,m}$
be the rank-three Coxeter group
 $$ \begin{align*} W_{k,n,m}=\bigg\langle r_1,r_2,r_3 \ \bigg\vert\ \begin{matrix} r_1^2=r_2^2=r_3^2=1,\\ (r_1 r_2)^k=(r_2 r_3)^n=(r_3 r_1)^m=1. \end{matrix} \ \bigg\rangle \end{align*} $$
$$ \begin{align*} W_{k,n,m}=\bigg\langle r_1,r_2,r_3 \ \bigg\vert\ \begin{matrix} r_1^2=r_2^2=r_3^2=1,\\ (r_1 r_2)^k=(r_2 r_3)^n=(r_3 r_1)^m=1. \end{matrix} \ \bigg\rangle \end{align*} $$
Let
![]() $W_{k,n,m}^+$
be its alternating subgroup, that is, the subgroup of elements with signature
$W_{k,n,m}^+$
be its alternating subgroup, that is, the subgroup of elements with signature
![]() $1$
. Let
$1$
. Let
![]() $c=(x_1 x_2 \cdots x_n)^m\in W(k,n,m)$
, which is central in
$c=(x_1 x_2 \cdots x_n)^m\in W(k,n,m)$
, which is central in
![]() $W(k,n,m)$
. Then we show (see Theorem 3.3) the following theorem.
$W(k,n,m)$
. Then we show (see Theorem 3.3) the following theorem.
Theorem 1.4. The group
![]() $W(k,n,m)$
is a central extension of
$W(k,n,m)$
is a central extension of
![]() $W_{k,n,m}^+$
by the subgroup
$W_{k,n,m}^+$
by the subgroup
![]() $\langle c \rangle $
. That is, we have a short exact sequence
$\langle c \rangle $
. That is, we have a short exact sequence
In most cases, the group
![]() $W_{k,n,m}$
is infinite and irreducible. The determination of the center of a toric reflection group uses the following result, which is of independent interest (see Proposition 3.1).
$W_{k,n,m}$
is infinite and irreducible. The determination of the center of a toric reflection group uses the following result, which is of independent interest (see Proposition 3.1).
Proposition 1.5 (Center of alternating subgroups of Coxeter groups)
Let
![]() $(W,S)$
be a Coxeter system of rank at least
$(W,S)$
be a Coxeter system of rank at least
![]() $3$
. Let
$3$
. Let
![]() $W^+$
be the alternating subgroup of W. Then the center
$W^+$
be the alternating subgroup of W. Then the center
![]() $Z(W^+)$
of
$Z(W^+)$
of
![]() $W^+$
is included in the center of W. In particular, if
$W^+$
is included in the center of W. In particular, if
![]() $(W,S)$
is infinite, irreducible, and of rank at least three, then
$(W,S)$
is infinite, irreducible, and of rank at least three, then
![]() $Z(W^+)$
is trivial.
$Z(W^+)$
is trivial.
Together with Theorem 1.4 and a case-by-case check in the cases where
![]() $W_{k,n,m}$
is finite, Proposition 1.5 yields (see Theorem 3.3 below) the following corollary.
$W_{k,n,m}$
is finite, Proposition 1.5 yields (see Theorem 3.3 below) the following corollary.
Corollary 1.6 (Center of toric reflection groups)
The center of
![]() $W(k,n,m)$
is cyclic, generated by c.
$W(k,n,m)$
is cyclic, generated by c.
In the case where
![]() $W(k,n,m)$
is infinite, we do not know whether c has finite order or not (see Remark 3.8). An explicit identification of the center inside the group together with Theorem 1.4 would show that the groups
$W(k,n,m)$
is infinite, we do not know whether c has finite order or not (see Remark 3.8). An explicit identification of the center inside the group together with Theorem 1.4 would show that the groups
![]() $W(k,n,m)$
have solvable word problems—see Question 3.9 and the discussion above it.
$W(k,n,m)$
have solvable word problems—see Question 3.9 and the discussion above it.
In the case where
![]() $W(k,n,m)$
is finite, Theorem 1.4 together with Corollary 1.6 give for the groups listed above a new and more general explanation for the known description of the quotient
$W(k,n,m)$
is finite, Theorem 1.4 together with Corollary 1.6 give for the groups listed above a new and more general explanation for the known description of the quotient
![]() $W(k,n,m)/Z(W(k,n,m))$
, as we see that it is isomorphic to the alternating subgroup of a Coxeter group that can be attached in a uniform way to all the concerned finite complex reflection groups. Note that when
$W(k,n,m)/Z(W(k,n,m))$
, as we see that it is isomorphic to the alternating subgroup of a Coxeter group that can be attached in a uniform way to all the concerned finite complex reflection groups. Note that when
![]() $W(k,n,m)$
is finite, it is known that
$W(k,n,m)$
is finite, it is known that
![]() $k-1$
is the number of conjugacy classes of reflections in
$k-1$
is the number of conjugacy classes of reflections in
![]() $W(k,n,m)$
, and that n is the reflection rank of
$W(k,n,m)$
, and that n is the reflection rank of
![]() $W(k,n,m)$
, that is, the minimal number of reflections that are needed to generate
$W(k,n,m)$
, that is, the minimal number of reflections that are needed to generate
![]() $W(k,n,m)$
. For arbitrary
$W(k,n,m)$
. For arbitrary
![]() $W(k,n,m)$
, we see that it is still true that
$W(k,n,m)$
, we see that it is still true that
![]() $k-1$
is the number of conjugacy classes of reflections, but we do not know whether n is equal to the reflection rank of
$k-1$
is the number of conjugacy classes of reflections, but we do not know whether n is equal to the reflection rank of
![]() $W(k,n,m)$
or not—see Remark 4.8. A positive answer would be a first step toward another proof of the classification of toric reflection groups given in Theorem 1.2 that may avoid the recourse to Coxeter groups—which has other advantages, as for instance Coxeter groups of rank three have nice geometric realizations. This would also give another way of showing that the meridional rank of the torus knot
$W(k,n,m)$
or not—see Remark 4.8. A positive answer would be a first step toward another proof of the classification of toric reflection groups given in Theorem 1.2 that may avoid the recourse to Coxeter groups—which has other advantages, as for instance Coxeter groups of rank three have nice geometric realizations. This would also give another way of showing that the meridional rank of the torus knot
![]() $T_{n,m}$
(
$T_{n,m}$
(
![]() $n<m$
) is equal to n (established in [Reference Rost and Zieschang30]).
$n<m$
) is equal to n (established in [Reference Rost and Zieschang30]).
The paper is organized as follows. Note that since the results are not always proven in the same order as they appear in the introduction, and sometimes require more notation than what we introduced above, we have a different numbering of the results in the rest of the paper, and sometimes a slightly different formulation. In Section 2, we recall from [Reference Achar and Aubert2] a few basic results on J-groups, and show that toric reflection groups are J-groups, allowing one to consider toric reflection groups as (a generalization of) complex reflection groups of rank two. In Section 3, we identify the center of toric reflection groups and link them as explained above to alternating subgroups of Coxeter groups of rank three. In Section 4, we use the previously established results to classify toric reflection groups; a main ingredient to this end is the study of finite subgroups of (alternating subgroups of) Coxeter groups of rank three.
2 J-groups and toric reflection groups
In this section, we first recall the definition and basic properties of J-groups in Section 2.1. These groups, which are infinite in general, were introduced by Achar and Aubert in [Reference Achar and Aubert2] as a generalization of finite complex reflection groups of rank two. They are defined as certain normal subgroups of a family of groups defined by generators and relations, which are themselves J-groups. We then show that toric reflection groups are J-groups of a certain kind in Section 2.2 by giving an explicit presentation by generators and relations for these J-groups using the Reidemeister–Schreier algorithm. Finally, in Section 2.3, we discuss the faithfulness of Achar and Aubert’s representation for this family of groups.
2.1 J-groups: definition and basic properties
Let
![]() $a,b,c\geq 2$
. Let
$a,b,c\geq 2$
. Let
![]() $J(\begin {smallmatrix} a & b & c \\ ~ & ~ & ~ \end {smallmatrix})$
be the group defined by the following presentation:
$J(\begin {smallmatrix} a & b & c \\ ~ & ~ & ~ \end {smallmatrix})$
be the group defined by the following presentation:
 $$ \begin{align*}J\begin{pmatrix} a & b & c \\ ~ & ~ & ~ \end{pmatrix}:=\langle s,t,u \ \vert \ s^a = t^b = u^c=1,\ stu=tus=ust \rangle.\end{align*} $$
$$ \begin{align*}J\begin{pmatrix} a & b & c \\ ~ & ~ & ~ \end{pmatrix}:=\langle s,t,u \ \vert \ s^a = t^b = u^c=1,\ stu=tus=ust \rangle.\end{align*} $$
Let
![]() $a',b',c'$
be three pairwise coprime positive integers, such that
$a',b',c'$
be three pairwise coprime positive integers, such that
![]() $k'$
divides k for all
$k'$
divides k for all
![]() $k\in \{a,b,c\}$
. Let
$k\in \{a,b,c\}$
. Let
![]() $J(\begin {smallmatrix} a & b & c \\ a' & b' & c'\! \end {smallmatrix})$
be the normal closure in
$J(\begin {smallmatrix} a & b & c \\ a' & b' & c'\! \end {smallmatrix})$
be the normal closure in
![]() $J(\begin {smallmatrix} a & b & c \\ ~ & ~ & ~ \end {smallmatrix})$
of the elements
$J(\begin {smallmatrix} a & b & c \\ ~ & ~ & ~ \end {smallmatrix})$
of the elements
![]() $s^{a'}, t^{b'}$
, and
$s^{a'}, t^{b'}$
, and
![]() $u^{c'}$
. These groups were defined by Achar and Aubert in [Reference Achar and Aubert2], and are called J-groups. Note that
$u^{c'}$
. These groups were defined by Achar and Aubert in [Reference Achar and Aubert2], and are called J-groups. Note that
![]() $J(\begin {smallmatrix} a & b & c \\ 1 & 1 & 1 \end {smallmatrix})=J(\begin {smallmatrix} a & b & c \\~ & ~ & ~ \end {smallmatrix})$
, and hence
$J(\begin {smallmatrix} a & b & c \\ 1 & 1 & 1 \end {smallmatrix})=J(\begin {smallmatrix} a & b & c \\~ & ~ & ~ \end {smallmatrix})$
, and hence
![]() $J(\begin {smallmatrix} a & b & c \\~ & ~ & ~ \end {smallmatrix})$
is itself a J-group, and we may call it the parent J-group of
$J(\begin {smallmatrix} a & b & c \\~ & ~ & ~ \end {smallmatrix})$
is itself a J-group, and we may call it the parent J-group of
![]() $J(\begin {smallmatrix} a & b & c \\ a' & b' & c' \end {smallmatrix})$
; in general, and also for other J-groups, the parameters equal to
$J(\begin {smallmatrix} a & b & c \\ a' & b' & c' \end {smallmatrix})$
; in general, and also for other J-groups, the parameters equal to
![]() $1$
are omitted in the second row of parameters.
$1$
are omitted in the second row of parameters.
Recall that a complex reflection group is a (finite) subgroup
![]() $W\subseteq \mathrm {GL}_n(\mathbb {C})$
generated by (pseudo-)reflections, that is, elements of finite order whose space of fixed points is a hyperplane in
$W\subseteq \mathrm {GL}_n(\mathbb {C})$
generated by (pseudo-)reflections, that is, elements of finite order whose space of fixed points is a hyperplane in
![]() $\mathbb {C}^n$
—see [Reference Broué11, Reference Lehrer and Taylor23] for basics on complex reflection groups. Achar and Aubert’s main result is the following.
$\mathbb {C}^n$
—see [Reference Broué11, Reference Lehrer and Taylor23] for basics on complex reflection groups. Achar and Aubert’s main result is the following.
Theorem 2.1 (See [Reference Achar and Aubert2, Theorem 1.2])
A J-group is finite if and only if it is a finite complex reflection group of rank two.
In the case where a J-group
![]() $H:=J(\begin {smallmatrix} a & b & c \\ a' & b' & c' \end {smallmatrix})$
is finite, it turns out that both H and
$H:=J(\begin {smallmatrix} a & b & c \\ a' & b' & c' \end {smallmatrix})$
is finite, it turns out that both H and
![]() $G:=J(\begin {smallmatrix} a & b & c \\ ~ & ~ & ~ \end {smallmatrix})$
are finite (see [Reference Achar and Aubert2]). In this case, the generators
$G:=J(\begin {smallmatrix} a & b & c \\ ~ & ~ & ~ \end {smallmatrix})$
are finite (see [Reference Achar and Aubert2]). In this case, the generators
![]() $s, t$
, and u are reflections, and since a power of a reflection is either the identity or a reflection and the set of reflections is stable by conjugation, the subgroup H is generated by reflections, that is, it is a reflection subgroup of G. In the case where G is infinite, it is shown in [Reference Achar and Aubert2] that one can still define a representation
$s, t$
, and u are reflections, and since a power of a reflection is either the identity or a reflection and the set of reflections is stable by conjugation, the subgroup H is generated by reflections, that is, it is a reflection subgroup of G. In the case where G is infinite, it is shown in [Reference Achar and Aubert2] that one can still define a representation
of G (and hence of H) where the generators of G act by reflections. However, as we see in Section 2.3, this representation is unfaithful in general when G is infinite. The elements
![]() $s,t$
, and u have orders
$s,t$
, and u have orders
![]() $a,b$
, and c in G (see the proof of Lemma 2.5).
$a,b$
, and c in G (see the proof of Lemma 2.5).
Definition 2.2. The reflections in
![]() $H=J(\begin {smallmatrix} a & b & c \\ a' & b' & c' \end {smallmatrix})\trianglelefteq J(\begin {smallmatrix} a & b & c \\ ~ & ~ & ~ \end {smallmatrix})=G$
are those elements of H that are G-conjugates of a power of
$H=J(\begin {smallmatrix} a & b & c \\ a' & b' & c' \end {smallmatrix})\trianglelefteq J(\begin {smallmatrix} a & b & c \\ ~ & ~ & ~ \end {smallmatrix})=G$
are those elements of H that are G-conjugates of a power of
![]() $s^{a'},t^{b'}$
, or
$s^{a'},t^{b'}$
, or
![]() $u^{c'}$
that is not the identity. We denote by
$u^{c'}$
that is not the identity. We denote by
![]() $R(H)$
the set of reflections in H.
$R(H)$
the set of reflections in H.
Definition 2.3. Let
![]() $G, G'$
be two J-groups with respective sets of reflections
$G, G'$
be two J-groups with respective sets of reflections
![]() $R, R'$
. Let
$R, R'$
. Let
![]() $\varphi : G\longrightarrow G'$
be a group homomorphism. We say that
$\varphi : G\longrightarrow G'$
be a group homomorphism. We say that
![]() $\varphi $
is a reflection homomorphism if
$\varphi $
is a reflection homomorphism if
![]() $\varphi (R)\subseteq R'$
. Another possible definition of reflection homomorphism could be to require that
$\varphi (R)\subseteq R'$
. Another possible definition of reflection homomorphism could be to require that
![]() $\varphi (R)\subseteq R'\cup \{1\}$
, which might be more suitable to study quotients, as done for instance in [Reference Maxwell26] in the case of finite Coxeter groups and their standard generators. In this paper, we only consider reflection isomorphisms, which are obviously the same in both categories. We say that G and
$\varphi (R)\subseteq R'\cup \{1\}$
, which might be more suitable to study quotients, as done for instance in [Reference Maxwell26] in the case of finite Coxeter groups and their standard generators. In this paper, we only consider reflection isomorphisms, which are obviously the same in both categories. We say that G and
![]() $G'$
are reflection isomorphic if there is a reflection homomorphism
$G'$
are reflection isomorphic if there is a reflection homomorphism
![]() $\varphi :G\longrightarrow G'$
that is a group isomorphism and such that
$\varphi :G\longrightarrow G'$
that is a group isomorphism and such that
![]() $\varphi (R)=R'$
.
$\varphi (R)=R'$
.
Remark 2.4. Note that permuting the columns of a J-group G yields another J-group
![]() $G'$
that is reflection isomorphic to G: a reflection isomorphism between
$G'$
that is reflection isomorphic to G: a reflection isomorphism between
![]() $J(\begin {smallmatrix} a & b & c\\ a'& b'& c'\end {smallmatrix})$
and
$J(\begin {smallmatrix} a & b & c\\ a'& b'& c'\end {smallmatrix})$
and
![]() $J(\begin {smallmatrix} b & a & c\\ b'& a'& c'\end {smallmatrix})$
is obtained by mapping s to
$J(\begin {smallmatrix} b & a & c\\ b'& a'& c'\end {smallmatrix})$
is obtained by mapping s to
![]() $t^{-1}$
, t to
$t^{-1}$
, t to
![]() $s^{-1}$
, and u to
$s^{-1}$
, and u to
![]() $u^{-1}$
, while a reflection isomorphism between
$u^{-1}$
, while a reflection isomorphism between
![]() $J(\begin {smallmatrix} a & b & c\\ a'& b'& c'\end {smallmatrix})$
and
$J(\begin {smallmatrix} a & b & c\\ a'& b'& c'\end {smallmatrix})$
and
![]() $J(\begin {smallmatrix} c & a & b\\ c'& a'& b'\end {smallmatrix})$
is obtained by mapping s to t, t to u, and u to s. These two reflection isomorphisms are enough to generate every permutation of the columns.
$J(\begin {smallmatrix} c & a & b\\ c'& a'& b'\end {smallmatrix})$
is obtained by mapping s to t, t to u, and u to s. These two reflection isomorphisms are enough to generate every permutation of the columns.
Lemma 2.5. No two elements in
![]() $\{s, s^2, \ldots , s^{a-1}, t, t^2, \ldots , t^{b-1}, u, u^2, \ldots , u^{c-1}\}$
are conjugate to each other in
$\{s, s^2, \ldots , s^{a-1}, t, t^2, \ldots , t^{b-1}, u, u^2, \ldots , u^{c-1}\}$
are conjugate to each other in
![]() $G=J(\begin {smallmatrix} a & b & c\\ ~& ~& ~\end {smallmatrix})$
. In particular, there are
$G=J(\begin {smallmatrix} a & b & c\\ ~& ~& ~\end {smallmatrix})$
. In particular, there are
![]() $a+b+c-3$
conjugacy classes of reflections in G.
$a+b+c-3$
conjugacy classes of reflections in G.
Proof. It suffices to note that the quotient of
![]() $J(\begin {smallmatrix} a & b & c\\ ~& ~& ~\end {smallmatrix})$
by the normal subgroup
$J(\begin {smallmatrix} a & b & c\\ ~& ~& ~\end {smallmatrix})$
by the normal subgroup
![]() $\langle \langle a \rangle \rangle $
normally generated by a is isomorphic to the abelian group
$\langle \langle a \rangle \rangle $
normally generated by a is isomorphic to the abelian group
![]() $\mathbb {Z}/b\mathbb {Z}\times \mathbb {Z}/c\mathbb {Z}$
, with t having image
$\mathbb {Z}/b\mathbb {Z}\times \mathbb {Z}/c\mathbb {Z}$
, with t having image
![]() $(\overline {1},\overline {0})$
and u having image
$(\overline {1},\overline {0})$
and u having image
![]() $(\overline {0},\overline {1})$
. This shows that no two elements in
$(\overline {0},\overline {1})$
. This shows that no two elements in
are conjugate in G, as their images in the abelian quotient would have to be equal. Arguing similarly with the normal subgroups
![]() $\langle \langle b \rangle \rangle $
and
$\langle \langle b \rangle \rangle $
and
![]() $\langle \langle c \rangle \rangle $
, we get the claim.
$\langle \langle c \rangle \rangle $
, we get the claim.
Note that this also shows that
![]() $s, t$
, and u have orders
$s, t$
, and u have orders
![]() $a, b$
, and c in G.
$a, b$
, and c in G.
Lemma 2.6. With the notation of Definition 2.2, we have
![]() $R(H)=R(G)\cap H$
.
$R(H)=R(G)\cap H$
.
Proof. It is clear that
![]() $R(H)\subseteq R(G)\cap H$
. Conversely, let
$R(H)\subseteq R(G)\cap H$
. Conversely, let
![]() $wr^n w^{-1}\in R(G)\cap H$
, with
$wr^n w^{-1}\in R(G)\cap H$
, with
![]() $r\in \{s,t,u\}$
and n not divisible by
$r\in \{s,t,u\}$
and n not divisible by
![]() $o(r):=\mathrm {order}(r)$
. As
$o(r):=\mathrm {order}(r)$
. As
![]() $H\trianglelefteq G$
, we have
$H\trianglelefteq G$
, we have
![]() $r^n\in H$
. Assume without loss of generality that
$r^n\in H$
. Assume without loss of generality that
![]() $r=s$
. It remains to show that
$r=s$
. It remains to show that
![]() $a'$
divides n. If not, then there is
$a'$
divides n. If not, then there is
![]() $1\leq a"< a'$
such that
$1\leq a"< a'$
such that
![]() $s^{a"}\in H$
. However,
$s^{a"}\in H$
. However,
 $$ \begin{align*}G / H \cong J\begin{pmatrix}a' & b' & c'\\ ~& ~& ~\end{pmatrix},\end{align*} $$
$$ \begin{align*}G / H \cong J\begin{pmatrix}a' & b' & c'\\ ~& ~& ~\end{pmatrix},\end{align*} $$
and since the image of s in this quotient has order
![]() $a'$
, one cannot have
$a'$
, one cannot have
![]() $s^{a"}\in H$
, which is a contradiction. Hence,
$s^{a"}\in H$
, which is a contradiction. Hence,
![]() $a'$
divides n, and
$a'$
divides n, and
![]() $wr^n w^{-1}\in R(H)$
.
$wr^n w^{-1}\in R(H)$
.
Definition 2.7. Let H be a J-group. Define
![]() $\mathcal {H}(H)$
to be the quotient set of
$\mathcal {H}(H)$
to be the quotient set of
![]() $R(H)$
by the transitive closure of the relation
$R(H)$
by the transitive closure of the relation
![]() $r^n\sim r^m$
for all
$r^n\sim r^m$
for all
![]() $r\in R(H)$
and
$r\in R(H)$
and
![]() $1\leq n,m< o(r)$
. An element
$1\leq n,m< o(r)$
. An element
![]() $\mathcal {H}$
of
$\mathcal {H}$
of
![]() $\mathcal {H}(H)$
is called a reflecting hyperplane (attached to any reflection
$\mathcal {H}(H)$
is called a reflecting hyperplane (attached to any reflection
![]() $r\in R(H)$
such that the class
$r\in R(H)$
such that the class
![]() $[r]$
of r modulo
$[r]$
of r modulo
![]() $\sim $
is equal to
$\sim $
is equal to
![]() $\mathcal {H}$
). Note that the action of H on
$\mathcal {H}$
). Note that the action of H on
![]() $R(H)$
by conjugation induces an action of H on
$R(H)$
by conjugation induces an action of H on
![]() $\mathcal {H}(H)$
—more generally, if H has parent J-group G, then since H is normal in G, we have an action of G on
$\mathcal {H}(H)$
—more generally, if H has parent J-group G, then since H is normal in G, we have an action of G on
![]() $\mathcal {H}(H)$
.
$\mathcal {H}(H)$
.
Lemma 2.8. If a J-group
![]() $H\neq 1$
has a single H-conjugacy class of reflecting hyperplanes, then up to permutation of the columns, H is of the form
$H\neq 1$
has a single H-conjugacy class of reflecting hyperplanes, then up to permutation of the columns, H is of the form
![]() $J(\begin {smallmatrix} a & b & c\\ a'& b& c\end {smallmatrix})$
, where
$J(\begin {smallmatrix} a & b & c\\ a'& b& c\end {smallmatrix})$
, where
![]() $a'\neq a$
,
$a'\neq a$
,
![]() $b < c$
.
$b < c$
.
Proof. Given a J-group
![]() $H=J(\begin {smallmatrix} a & b & c\\ a'& b'& c'\end {smallmatrix})$
, if
$H=J(\begin {smallmatrix} a & b & c\\ a'& b'& c'\end {smallmatrix})$
, if
![]() $i'<i$
for more than one integer
$i'<i$
for more than one integer
![]() $i\in \{a,b,c\}$
, say a and b, then both
$i\in \{a,b,c\}$
, say a and b, then both
![]() $1\neq s^{a'}$
and
$1\neq s^{a'}$
and
![]() $1\neq t^{b'}$
lie in
$1\neq t^{b'}$
lie in
![]() $H\trianglelefteq G=J(\begin {smallmatrix} a & b & c\\ ~& ~& ~\end {smallmatrix})$
. For
$H\trianglelefteq G=J(\begin {smallmatrix} a & b & c\\ ~& ~& ~\end {smallmatrix})$
. For
![]() $r\in R(H)$
, by Lemma 2.5, the reflection r is conjugate (in G) to exactly one nontrivial power of a generator in
$r\in R(H)$
, by Lemma 2.5, the reflection r is conjugate (in G) to exactly one nontrivial power of a generator in
![]() $\{s,t,u\}$
and hence, all reflections
$\{s,t,u\}$
and hence, all reflections
![]() $r^m$
for
$r^m$
for
![]() $1\leq m <o(r)$
are conjugate in G to a power of the same generator. Now for any
$1\leq m <o(r)$
are conjugate in G to a power of the same generator. Now for any
![]() $r\in R(H)$
such that
$r\in R(H)$
such that
![]() $[r]$
lies in the H-conjugacy class of
$[r]$
lies in the H-conjugacy class of
![]() $[s^{a'}]$
, the reflection r is conjugate (in G) to a power of s. Similarly, for any
$[s^{a'}]$
, the reflection r is conjugate (in G) to a power of s. Similarly, for any
![]() $r\in R(H)$
such that
$r\in R(H)$
such that
![]() $[r]$
lies in the H-conjugacy class of
$[r]$
lies in the H-conjugacy class of
![]() $[t^{b'}]$
, the reflection r is conjugate (in G) to a power of t. It follows that the H-conjugacy classes of
$[t^{b'}]$
, the reflection r is conjugate (in G) to a power of t. It follows that the H-conjugacy classes of
![]() $[t^{b'}]$
and
$[t^{b'}]$
and
![]() $[s^{a'}]$
are distinct in G (and a fortiori in H), since if
$[s^{a'}]$
are distinct in G (and a fortiori in H), since if
![]() $[r]$
was a hyperplane in both classes, then r would be conjugate (in G) to both a power of s and a power of t, which by Lemma 2.5 is excluded.
$[r]$
was a hyperplane in both classes, then r would be conjugate (in G) to both a power of s and a power of t, which by Lemma 2.5 is excluded.
Hence, we have that H is of the form
![]() $J(\begin {smallmatrix} a & b & c\\ a'& b& c\end {smallmatrix})$
, where
$J(\begin {smallmatrix} a & b & c\\ a'& b& c\end {smallmatrix})$
, where
![]() $a'<a$
. Note that
$a'<a$
. Note that
![]() $b\neq c$
as
$b\neq c$
as
![]() $b'\neq c'$
by definition. Using also Remark 2.4, this concludes the proof.
$b'\neq c'$
by definition. Using also Remark 2.4, this concludes the proof.
Note that it is not clear a priori that every J-group of the form
![]() $H=J(\begin {smallmatrix} a & b & c\\ a'& b& c\end {smallmatrix})$
as above has a single conjugacy class of reflecting hyperplanes: by definition, the generators of H are all conjugate in G to a power of s, but it is not clear that they are in fact conjugate in H to a power of s. We show in Corollary 2.13 that this holds at least for
$H=J(\begin {smallmatrix} a & b & c\\ a'& b& c\end {smallmatrix})$
as above has a single conjugacy class of reflecting hyperplanes: by definition, the generators of H are all conjugate in G to a power of s, but it is not clear that they are in fact conjugate in H to a power of s. We show in Corollary 2.13 that this holds at least for
![]() $a'=1$
, using Theorem 2.12 and the following proposition.
$a'=1$
, using Theorem 2.12 and the following proposition.
Proposition 2.9. Let
![]() $H=J(\begin {smallmatrix} a & b & c\\ & b& c\end {smallmatrix})$
with
$H=J(\begin {smallmatrix} a & b & c\\ & b& c\end {smallmatrix})$
with
![]() $a,b,c\geq 2$
.
$a,b,c\geq 2$
.
-
(1) The reflections
 $x_i:=t^{i-1} s t^{-i+1}$
, where
$x_i:=t^{i-1} s t^{-i+1}$
, where
 $i=1,2, \ldots , b$
, generate H (as a group).
$i=1,2, \ldots , b$
, generate H (as a group). -
(2) Every reflection in H is a conjugate in H of a nontrivial power of some
 $x_i$
.
$x_i$
.
Proof. Since all the elements
![]() $x_i$
lie in H and
$x_i$
lie in H and
![]() $H\trianglelefteq G=J(\begin {smallmatrix} a & b & c\\ ~& ~& ~\end {smallmatrix})$
, their conjugates by
$H\trianglelefteq G=J(\begin {smallmatrix} a & b & c\\ ~& ~& ~\end {smallmatrix})$
, their conjugates by
![]() $s, t$
, and u again lie in H. We begin by showing that an element of the form
$s, t$
, and u again lie in H. We begin by showing that an element of the form
![]() $g x_i g^{-1}$
, where
$g x_i g^{-1}$
, where
![]() $g\in G$
can be rewritten in the form
$g\in G$
can be rewritten in the form
![]() $h x_j h^{-1}$
for some j and some element h lying in the subgroup
$h x_j h^{-1}$
for some j and some element h lying in the subgroup
![]() $H'\subseteq H$
generated by the elements
$H'\subseteq H$
generated by the elements
![]() $x_i$
. Note that by induction on the length of a word for g in
$x_i$
. Note that by induction on the length of a word for g in
![]() $\{s^{\pm 1}, t^{\pm 1}, u^{\pm 1}\}$
, it is enough to show it for
$\{s^{\pm 1}, t^{\pm 1}, u^{\pm 1}\}$
, it is enough to show it for
![]() $g\in \{s^{\pm 1},t^{\pm 1},u^{\pm 1}\}$
. For
$g\in \{s^{\pm 1},t^{\pm 1},u^{\pm 1}\}$
. For
![]() $g=s^{\pm 1}$
, we have
$g=s^{\pm 1}$
, we have
![]() $s^{\pm 1} x_i s^{\mp 1}=x_1^{\pm 1} x_i x_1^{\mp 1}$
as
$s^{\pm 1} x_i s^{\mp 1}=x_1^{\pm 1} x_i x_1^{\mp 1}$
as
![]() $s=x_1$
. We have
$s=x_1$
. We have
![]() $t^{\pm 1} x_i t^{\mp {1}}=x_{i\pm {1}}$
for all
$t^{\pm 1} x_i t^{\mp {1}}=x_{i\pm {1}}$
for all
![]() $i=1, \ldots , b$
(with the convention that
$i=1, \ldots , b$
(with the convention that
![]() $x_{b+j}=x_j$
). Using that
$x_{b+j}=x_j$
). Using that
![]() $stu$
is central in G,
$stu$
is central in G,
and a similar computation shows that
![]() $u^{-1} x_i u=x_1 x_{i+1} x_1^{-1}$
.
$u^{-1} x_i u=x_1 x_{i+1} x_1^{-1}$
.
Now H is generated by its reflections, that is, by the conjugates in G of the nontrivial powers of
![]() $s=x_1$
. However, by the observation above, every element of the form
$s=x_1$
. However, by the observation above, every element of the form
![]() $g x_1^\ell g^{-1}$
can be rewritten in the form
$g x_1^\ell g^{-1}$
can be rewritten in the form
![]() $h x_i^{\ell } h^{-1}$
for some i and some h in
$h x_i^{\ell } h^{-1}$
for some i and some h in
![]() $H'$
. It follows that the elements
$H'$
. It follows that the elements
![]() $x_i$
generate H, and hence that
$x_i$
generate H, and hence that
![]() $H'=H$
. The second point also follows.
$H'=H$
. The second point also follows.
2.2 Toric reflection groups are J-groups
Let
![]() $k,n,m\geq 2$
with
$k,n,m\geq 2$
with
![]() $n<m$
and
$n<m$
and
![]() $n,m$
coprime. Recall from the introduction that the toric reflection group
$n,m$
coprime. Recall from the introduction that the toric reflection group
![]() $W(k,n,m)$
is defined by the presentation
$W(k,n,m)$
is defined by the presentation
 $$ \begin{align} W(k,n,m):=\left\langle x_1, x_2, \ldots, x_n \ \vert\ \begin{matrix} x_i^k=1~\text{for}~i=1, \ldots, n,\\ \underbrace{x_1 x_2 \cdots}_{m~\text{factors}} = \underbrace{x_2 x_3\cdots}_{m~\text{factors}} = \cdots = \underbrace{x_n x_1 \cdots}_{m~\text{factors}} \end{matrix} \right\rangle.\end{align} $$
$$ \begin{align} W(k,n,m):=\left\langle x_1, x_2, \ldots, x_n \ \vert\ \begin{matrix} x_i^k=1~\text{for}~i=1, \ldots, n,\\ \underbrace{x_1 x_2 \cdots}_{m~\text{factors}} = \underbrace{x_2 x_3\cdots}_{m~\text{factors}} = \cdots = \underbrace{x_n x_1 \cdots}_{m~\text{factors}} \end{matrix} \right\rangle.\end{align} $$
In particular, the group
![]() $W(k,n,m)$
is a quotient of the torus knot group
$W(k,n,m)$
is a quotient of the torus knot group
![]() $G(n,m)$
as the above presentation is obtained from the classical Presentation (1-2) of
$G(n,m)$
as the above presentation is obtained from the classical Presentation (1-2) of
![]() $G(n,m)$
by adding the relations
$G(n,m)$
by adding the relations
![]() $x_i^k=1$
.
$x_i^k=1$
.
Definition 2.10. The set of reflections in
![]() $W(k,n,m)$
, denoted R, is the set of those elements in
$W(k,n,m)$
, denoted R, is the set of those elements in
![]() $W(k,n,m)$
which are conjugate to a nontrivial power of one of the elements
$W(k,n,m)$
which are conjugate to a nontrivial power of one of the elements
![]() $x_i$
, that is,
$x_i$
, that is,
We see later that all the elements
![]() $x_i$
have order k. Given two toric reflection groups
$x_i$
have order k. Given two toric reflection groups
![]() $W, W'$
with respective sets of reflections
$W, W'$
with respective sets of reflections
![]() $R, R'$
, we say that a group isomorphism
$R, R'$
, we say that a group isomorphism
![]() ${\varphi : W\longrightarrow W'}$
is a reflection isomorphism if
${\varphi : W\longrightarrow W'}$
is a reflection isomorphism if
![]() $\varphi (R)=R'$
, and write
$\varphi (R)=R'$
, and write
![]() $W\cong _{\mathrm {ref}} W'$
.
$W\cong _{\mathrm {ref}} W'$
.
Remark 2.11. Observe that Presentation (2-1) could be given as well for
![]() $m<n$
. We explain why we assume that
$m<n$
. We explain why we assume that
![]() $n<m$
in most statements. In fact, one has
$n<m$
in most statements. In fact, one has
![]() ${G(n,m)\cong G(m,n)}$
since the torus knots
${G(n,m)\cong G(m,n)}$
since the torus knots
![]() $T_{n,m}$
and
$T_{n,m}$
and
![]() $T_{m,n}$
are isotopic (see for instance [Reference Burde, Zieschang and Heusener13, Proposition 3.37]). By writing down explicitly an isomorphism between
$T_{m,n}$
are isotopic (see for instance [Reference Burde, Zieschang and Heusener13, Proposition 3.37]). By writing down explicitly an isomorphism between
![]() $G(n,m)$
and
$G(n,m)$
and
![]() $G(m,n)$
, it is not hard to see that it induces a reflection isomorphism
$G(m,n)$
, it is not hard to see that it induces a reflection isomorphism
![]() $W(k,n,m)\cong _{\mathrm {ref}} W(k,m,n)$
. We see in this section another explanation for this isomorphism, by realizing toric reflection groups as J-groups. More precisely, this is a consequence of the first point of Corollary 2.13 together with the reflection isomorphism
$W(k,n,m)\cong _{\mathrm {ref}} W(k,m,n)$
. We see in this section another explanation for this isomorphism, by realizing toric reflection groups as J-groups. More precisely, this is a consequence of the first point of Corollary 2.13 together with the reflection isomorphism
 $$ \begin{align*}J\begin{pmatrix} k & n & m\\ ~& n& m\end{pmatrix}\cong_{\mathrm{ref}} J\begin{pmatrix} k & m & n\\ ~& m& n\end{pmatrix}\end{align*} $$
$$ \begin{align*}J\begin{pmatrix} k & n & m\\ ~& n& m\end{pmatrix}\cong_{\mathrm{ref}} J\begin{pmatrix} k & m & n\\ ~& m& n\end{pmatrix}\end{align*} $$
from Remark 2.4.
Theorem 2.12 (Toric reflection groups are J-groups)
Let
![]() $k, n, m\geq 2$
with
$k, n, m\geq 2$
with
![]() $n,m$
coprime (we do not necessarily assume
$n,m$
coprime (we do not necessarily assume
![]() $n<m$
here), and let
$n<m$
here), and let
![]() $H=J(\begin {smallmatrix} k & n & m\\ ~& n& m\end {smallmatrix})\trianglelefteq J(\begin {smallmatrix} k & n & m\\ ~& ~& ~\end {smallmatrix})=G$
. Then H has a presentation with generators
$H=J(\begin {smallmatrix} k & n & m\\ ~& n& m\end {smallmatrix})\trianglelefteq J(\begin {smallmatrix} k & n & m\\ ~& ~& ~\end {smallmatrix})=G$
. Then H has a presentation with generators
![]() $x_1, x_2, \ldots , x_n$
and relations (indices are taken modulo n)
$x_1, x_2, \ldots , x_n$
and relations (indices are taken modulo n)
 $$ \begin{align*} &x_i^k=1, \quad \text{for all } i=1, \ldots, n,\\ &x_1 x_2 \cdots x_m = x_i x_{i+1} \cdots x_{i+m-1}, \quad \text{for all } i=2, \ldots, n. \end{align*} $$
$$ \begin{align*} &x_i^k=1, \quad \text{for all } i=1, \ldots, n,\\ &x_1 x_2 \cdots x_m = x_i x_{i+1} \cdots x_{i+m-1}, \quad \text{for all } i=2, \ldots, n. \end{align*} $$
If
![]() $n<m$
, we therefore have
$n<m$
, we therefore have
![]() $W(k,n,m)\cong H$
. In terms of the generators of G, we have
$W(k,n,m)\cong H$
. In terms of the generators of G, we have
![]() $x_i=t^{i-1} s t^{-i+1}$
for all
$x_i=t^{i-1} s t^{-i+1}$
for all
![]() $i=1, \ldots , n$
.
$i=1, \ldots , n$
.
Corollary 2.13. Let
![]() $H=J(\begin {smallmatrix} k & n & m\\ ~& n& m\end {smallmatrix})$
, with
$H=J(\begin {smallmatrix} k & n & m\\ ~& n& m\end {smallmatrix})$
, with
![]() $k,n,m$
as in Theorem 2.12.
$k,n,m$
as in Theorem 2.12.
-
(1) Let R be the set of reflections in
 $W(k,n,m)$
and
$W(k,n,m)$
and
 $R'$
be the set of reflections in
$R'$
be the set of reflections in
 $H=J(\begin {smallmatrix} k & n & m\\ ~& n& m\end {smallmatrix})$
. The isomorphism
$H=J(\begin {smallmatrix} k & n & m\\ ~& n& m\end {smallmatrix})$
. The isomorphism
 $\varphi : W(k,n,m)\overset {\cong }{\longrightarrow } H, x_i \mapsto t^{i-1} s t^{-i+1}$
from Theorem 2.12 satisfies
$\varphi : W(k,n,m)\overset {\cong }{\longrightarrow } H, x_i \mapsto t^{i-1} s t^{-i+1}$
from Theorem 2.12 satisfies
 $\varphi (R)=R'$
. In other words, it is an isomorphism of ‘reflection groups’.
$\varphi (R)=R'$
. In other words, it is an isomorphism of ‘reflection groups’. -
(2) There is a single H-conjugacy class of reflecting hyperplanes in H.
Proof. All the elements
![]() $t^{i-1} s t^{-i+1}$
are reflections in H, and hence we have
$t^{i-1} s t^{-i+1}$
are reflections in H, and hence we have
![]() $\varphi (R)\subseteq R'$
. Conversely, let r be a reflection in H. Then by the second point of Proposition 2.9, it is conjugate in H to a nontrivial power of some
$\varphi (R)\subseteq R'$
. Conversely, let r be a reflection in H. Then by the second point of Proposition 2.9, it is conjugate in H to a nontrivial power of some
![]() $x_i$
, and hence
$x_i$
, and hence
![]() $\varphi ^{-1}(R')\subseteq R$
.
$\varphi ^{-1}(R')\subseteq R$
.
By definition of H, we know that all the reflecting hyperplanes in H are conjugate in
![]() $G=J(\begin {smallmatrix} k & n & m\\ ~& ~& ~\end {smallmatrix})$
, but it is not obvious that they are conjugate in H. However, by the second point of Proposition 2.9, we know that every reflection in H is conjugate in H to a nontrivial power of some
$G=J(\begin {smallmatrix} k & n & m\\ ~& ~& ~\end {smallmatrix})$
, but it is not obvious that they are conjugate in H. However, by the second point of Proposition 2.9, we know that every reflection in H is conjugate in H to a nontrivial power of some
![]() $x_i$
. To conclude the proof, it therefore suffices to show that all the elements
$x_i$
. To conclude the proof, it therefore suffices to show that all the elements
![]() $x_i$
are conjugate in H. We use Theorem 2.12 to this end: since n and m are coprime, all the elements
$x_i$
are conjugate in H. We use Theorem 2.12 to this end: since n and m are coprime, all the elements
![]() $x_i$
are conjugate to each other in
$x_i$
are conjugate to each other in
![]() $W(k,n,m)$
, as a consequence of the relations
$W(k,n,m)$
, as a consequence of the relations
The proof of Theorem 2.12 occupies the remainder of the section. It is obtained via an application of the Reidemeister–Schreier algorithm (see for instance [Reference Magnus, Karras and Solitar24]).
Example 2.14. For
![]() $k=2, n=3, m=4$
, we get the presentation
$k=2, n=3, m=4$
, we get the presentation
This is a presentation of the complex reflection group
![]() $G_{12}$
in Shephard–Todd notation (see for instance [Reference Broué11, Table A.3]), and we recover (as in [Reference Achar and Aubert2]) that
$G_{12}$
in Shephard–Todd notation (see for instance [Reference Broué11, Table A.3]), and we recover (as in [Reference Achar and Aubert2]) that
![]() $J(\begin {smallmatrix} 2 & 3 & 4\\ ~& 3& 4\end {smallmatrix})\cong G_{12}$
. Similarly, for the values of
$J(\begin {smallmatrix} 2 & 3 & 4\\ ~& 3& 4\end {smallmatrix})\cong G_{12}$
. Similarly, for the values of
![]() $k,n,m$
given in Table 1, we obtain all the finite toric reflection groups (the fact that they are the only finite toric groups follows from the classification given in [Reference Achar and Aubert2]). These are the finite complex reflection groups of rank two with a single conjugacy class of reflecting hyperplanes.
$k,n,m$
given in Table 1, we obtain all the finite toric reflection groups (the fact that they are the only finite toric groups follows from the classification given in [Reference Achar and Aubert2]). These are the finite complex reflection groups of rank two with a single conjugacy class of reflecting hyperplanes.
Table 1 Finite toric reflection groups.

Remark 2.15. It is well known that
![]() $G_{16}$
,
$G_{16}$
,
![]() $G_{20}$
, and
$G_{20}$
, and
![]() $G_{22}$
are normal subgroups of
$G_{22}$
are normal subgroups of
![]() ${G_{19}=J(\begin {smallmatrix} 2 & 3 & 5\\ ~& ~& ~\end {smallmatrix})}$
, that
${G_{19}=J(\begin {smallmatrix} 2 & 3 & 5\\ ~& ~& ~\end {smallmatrix})}$
, that
![]() $G_4$
is a normal subgroup of
$G_4$
is a normal subgroup of
![]() $G_7=J(\begin {smallmatrix} 2 & 3 & 3\\ ~& ~& ~\end {smallmatrix})$
, and that
$G_7=J(\begin {smallmatrix} 2 & 3 & 3\\ ~& ~& ~\end {smallmatrix})$
, and that
![]() $G_8$
and
$G_8$
and
![]() $G_{12}$
are normal subgroups of
$G_{12}$
are normal subgroups of
![]() $G_{11}=J(\begin {smallmatrix} 2 & 3 & 4\\ ~& ~& ~\end {smallmatrix})$
(see for instance [Reference Lehrer and Taylor23, Ch. 6]). In particular, Theorem 2.12 reproves this fact and gives a way to express the generators of these subgroups in terms of the generators of
$G_{11}=J(\begin {smallmatrix} 2 & 3 & 4\\ ~& ~& ~\end {smallmatrix})$
(see for instance [Reference Lehrer and Taylor23, Ch. 6]). In particular, Theorem 2.12 reproves this fact and gives a way to express the generators of these subgroups in terms of the generators of
![]() $G_{19}$
,
$G_{19}$
,
![]() $G_{7}$
, and
$G_{7}$
, and
![]() $G_{11}$
(see also [Reference Malle and Michel25, Table 1]).
$G_{11}$
(see also [Reference Malle and Michel25, Table 1]).
Let
![]() $G, H$
be as in Theorem 2.12. Note that as
$G, H$
be as in Theorem 2.12. Note that as
![]() $G/H\cong \mathbb {Z}/n\mathbb {Z} \times \mathbb {Z}/m\mathbb {Z}$
, a system of representatives of the (right) cosets modulo H is given by
$G/H\cong \mathbb {Z}/n\mathbb {Z} \times \mathbb {Z}/m\mathbb {Z}$
, a system of representatives of the (right) cosets modulo H is given by
![]() $H u^i t^j$
,
$H u^i t^j$
,
![]() $0\leq i < m$
,
$0\leq i < m$
,
![]() $0\leq j < n$
. Note that the set
$0\leq j < n$
. Note that the set
![]() $\mathcal {K}:=\{ u^i t^j\}_{0\leq i < m, 0 \leq j < n}$
yields a Schreier transversal for
$\mathcal {K}:=\{ u^i t^j\}_{0\leq i < m, 0 \leq j < n}$
yields a Schreier transversal for
![]() $G/H$
. For
$G/H$
. For
![]() $g\in G$
, we denote by
$g\in G$
, we denote by
![]() $\overline {g}$
the representative of
$\overline {g}$
the representative of
![]() $Hg$
in
$Hg$
in
![]() $\mathcal {K}$
. Recall that a system of generators for H is given by the elements of the form
$\mathcal {K}$
. Recall that a system of generators for H is given by the elements of the form
![]() $k x \overline {kx}^{-1}$
, where
$k x \overline {kx}^{-1}$
, where
![]() $k\in \mathcal {K}$
and
$k\in \mathcal {K}$
and
![]() $x\in \{s,t,u\}$
. For
$x\in \{s,t,u\}$
. For
![]() $x\in \{s,t,u\}$
and
$x\in \{s,t,u\}$
and
![]() $0\leq i < m$
,
$0\leq i < m$
,
![]() $0\leq j < n$
, we denote the generator
$0\leq j < n$
, we denote the generator
![]() $u^i t^j x \overline {u^i t^j x}^{-1}$
of H by
$u^i t^j x \overline {u^i t^j x}^{-1}$
of H by
![]() $x_{i,j}$
. Among this set of generators, some of them are the identity, namely:
$x_{i,j}$
. Among this set of generators, some of them are the identity, namely:
-
•
 $t_{i,j}=1$
for all
$t_{i,j}=1$
for all
 $0\leq i < m$
,
$0\leq i < m$
,
 $0\leq j < n$
;
$0\leq j < n$
; -
•
 $u_{i,0}=1$
for all
$u_{i,0}=1$
for all
 $0\leq i < m$
.
$0\leq i < m$
.
For simplicity of notation in the next proofs, it is convenient to consider the first subscript in
![]() $x_{i,j}$
modulo m and the second one modulo n, that is, to write
$x_{i,j}$
modulo m and the second one modulo n, that is, to write
![]() $x_{i+m,j}=x_{i,j}$
and
$x_{i+m,j}=x_{i,j}$
and
![]() $x_{i,j+n}=x_{i,j}$
for all
$x_{i,j+n}=x_{i,j}$
for all
![]() $i,j\in \mathbb {Z}$
.
$i,j\in \mathbb {Z}$
.
The graph given by the action of generators of G on (right) cosets modulo H is given in Figure 2. More precisely, if a generator
![]() $x\in \{s,t,u\}$
is such that
$x\in \{s,t,u\}$
is such that
![]() $(H u^i t^j)x=H u^{i'} t^{j'}$
, then we draw an arrow from the vertex
$(H u^i t^j)x=H u^{i'} t^{j'}$
, then we draw an arrow from the vertex
![]() $H u^i t^j$
to the vertex
$H u^i t^j$
to the vertex
![]() $H u^{i'} t^{j'}$
, indexed by
$H u^{i'} t^{j'}$
, indexed by
![]() $x_{i,j}$
. The plain arrows give the spanning tree corresponding to the Schreier transversal with respect to the generating set
$x_{i,j}$
. The plain arrows give the spanning tree corresponding to the Schreier transversal with respect to the generating set
![]() $\{s,t,u\}$
of G. In this case, the corresponding generator x is equal to
$\{s,t,u\}$
of G. In this case, the corresponding generator x is equal to
![]() $1$
, and we simply label the corresponding arrow by x. The reason for such a notation is that it becomes easy using this graph to write down the relations given by the Reidemeister–Schreier algorithm: one simply applies the defining relations of G at each vertex of the coset graph, following arrows from left to right: for instance, applying the relations
$1$
, and we simply label the corresponding arrow by x. The reason for such a notation is that it becomes easy using this graph to write down the relations given by the Reidemeister–Schreier algorithm: one simply applies the defining relations of G at each vertex of the coset graph, following arrows from left to right: for instance, applying the relations
![]() $stu=tus=ust$
at the vertex
$stu=tus=ust$
at the vertex
![]() $Hut$
(see Figure 1) yields the relations
$Hut$
(see Figure 1) yields the relations
as arrows labeled by t have their corresponding generator equal to
![]() $1$
.
$1$
.

Figure 1 Application of the relations
![]() $stu=tus=ust$
at the vertex
$stu=tus=ust$
at the vertex
![]() $Hut$
of the coset graph to obtain defining relations of H.
$Hut$
of the coset graph to obtain defining relations of H.
We get the following relations.
Relations coming from the relations
![]() $s^k=t^n=u^m=1$
. We get
$s^k=t^n=u^m=1$
. We get
Relations coming from the relations
![]() $stu=tus=ust$
.
$stu=tus=ust$
.
First column of the graph in Figure 2:
![]() $\underline{\text{Column } j, \text{where } 2\leq j \leq n-1}$
:
$\underline{\text{Column } j, \text{where } 2\leq j \leq n-1}$
:
Column n:
We have already seen in Proposition 2.9 that the elements
![]() $x_i:=t^{i-1}st^{1-i}$
(
$x_i:=t^{i-1}st^{1-i}$
(
![]() $1\leq i \leq n$
) generate H. Setting
$1\leq i \leq n$
) generate H. Setting
![]() $s_i:=s_{0,i}$
(
$s_i:=s_{0,i}$
(
![]() $1\leq i\leq n$
) and considering indices of the elements
$1\leq i\leq n$
) and considering indices of the elements
![]() $s_i$
modulo n, for all
$s_i$
modulo n, for all
![]() $1\leq i \leq n$
,
$1\leq i \leq n$
,
as
![]() $H t^{i-1}s=H \underbrace {t^{i-1}s t^{1-i}}_{\in H} t^{i-1}=H t^{i-1}$
. The next proposition therefore gives a new proof that the elements
$H t^{i-1}s=H \underbrace {t^{i-1}s t^{1-i}}_{\in H} t^{i-1}=H t^{i-1}$
. The next proposition therefore gives a new proof that the elements
![]() $x_1=s_0, x_2=s_1, \ldots , x_n=s_{n-1}$
are enough to generate H, and gives a formula for all the elements
$x_1=s_0, x_2=s_1, \ldots , x_n=s_{n-1}$
are enough to generate H, and gives a formula for all the elements
![]() $x_{i,j}$
of H in terms of these generators.
$x_{i,j}$
of H in terms of these generators.
Proposition 2.16. Let
![]() $0\leq \ell \leq m-1$
.
$0\leq \ell \leq m-1$
.
-
(1) Let
 $1\leq p \leq n$
. We have
$1\leq p \leq n$
. We have
 $s_{m-1-\ell , p-1}=s_0 s_1 \cdots s_{\ell } s_{p+\ell } s_{\ell }^{-1} s_{\ell -1}^{-1} \cdots s_0^{-1}$
.
$s_{m-1-\ell , p-1}=s_0 s_1 \cdots s_{\ell } s_{p+\ell } s_{\ell }^{-1} s_{\ell -1}^{-1} \cdots s_0^{-1}$
. -
(2) Let
 $1\leq p \leq n-1$
. We have
$1\leq p \leq n-1$
. We have
 $u_{m-1-\ell ,p}=s_0 s_1 \cdots s_{\ell } s_{p+\ell }^{-1} s_{\ell -1}^{-1} s_{\ell -2}^{-1} \cdots s_0^{-1}$
.
$u_{m-1-\ell ,p}=s_0 s_1 \cdots s_{\ell } s_{p+\ell }^{-1} s_{\ell -1}^{-1} s_{\ell -2}^{-1} \cdots s_0^{-1}$
.
In particular, the elements
![]() $s_i$
generate H.
$s_i$
generate H.

Figure 2 Coset graph of the (right) cosets of H with action of the generators of G, and corresponding generators of H. For clarity, we did not represent all the arrows, especially those with label
![]() $t_{i,n-1}=1$
,
$t_{i,n-1}=1$
,
![]() $u_{m-1, i}$
,
$u_{m-1, i}$
,
![]() $s_{i,j}$
. The plain arrows correspond to the spanning tree of the graph yielding the Schreier transversal (and have corresponding generator of H equal to
$s_{i,j}$
. The plain arrows correspond to the spanning tree of the graph yielding the Schreier transversal (and have corresponding generator of H equal to
![]() $1$
).
$1$
).
The proof of Proposition 2.16 is by induction on
![]() $\ell $
. The following lemma deals with the case
$\ell $
. The following lemma deals with the case
![]() $\ell =0$
.
$\ell =0$
.
Lemma 2.17.
-
(1) Let
 $1\leq p \leq n$
. We have
$1\leq p \leq n$
. We have
 $s_{m-1, p-1}=s_0 s_{p} s_0^{-1}$
.
$s_{m-1, p-1}=s_0 s_{p} s_0^{-1}$
. -
(2) Let
 $1\leq p \leq n-1$
. We have
$1\leq p \leq n-1$
. We have
 $u_{m-1, p}=s_0 s_p^{-1}$
.
$u_{m-1, p}=s_0 s_p^{-1}$
.
Proof. We argue by induction on p to show both statements for
![]() $1\leq p \leq n-1$
. Equation (2-4) (with
$1\leq p \leq n-1$
. Equation (2-4) (with
![]() $i=m-1$
) yields
$i=m-1$
) yields
from which we deduce that
![]() $u_{m-1,1}=s_0 s_1^{-1}$
and
$u_{m-1,1}=s_0 s_1^{-1}$
and
![]() $s_{m-1,0}= s_0 s_1 s_0^{-1}$
. Hence, the statement of the lemma holds true for
$s_{m-1,0}= s_0 s_1 s_0^{-1}$
. Hence, the statement of the lemma holds true for
![]() $p=1$
.
$p=1$
.
Assume that the result holds true for some
![]() $1\leq p \leq n-2$
. Equation (2-5) (with
$1\leq p \leq n-2$
. Equation (2-5) (with
![]() ${j=p+1}$
and
${j=p+1}$
and
![]() $i=m-1$
) yields
$i=m-1$
) yields
from which, by induction, we get
![]() $u_{m-1,p+1}=u_{m-1,p} s_p s_{p+1}^{-1}= s_0 s_p^{-1} s_p s_{p+1}^{-1}=s_0 s_{p+1}^{-1},$
and
$u_{m-1,p+1}=u_{m-1,p} s_p s_{p+1}^{-1}= s_0 s_p^{-1} s_p s_{p+1}^{-1}=s_0 s_{p+1}^{-1},$
and
![]() $s_{m-1,p}=u_{m-1,p+1} s_{p+1}u_{m-1,p+1}^{-1}=s_0 s_{p+1} s_0^{-1},$
and hence both statements also hold true for
$s_{m-1,p}=u_{m-1,p+1} s_{p+1}u_{m-1,p+1}^{-1}=s_0 s_{p+1} s_0^{-1},$
and hence both statements also hold true for
![]() $p+1$
. Therefore, the result holds true for all
$p+1$
. Therefore, the result holds true for all
![]() $1\leq p \leq n-1$
and it remains to check the first statement for
$1\leq p \leq n-1$
and it remains to check the first statement for
![]() $p=n$
, that is, that
$p=n$
, that is, that
![]() $s_{m-1,n-1}=s_0 s_{n} s_0^{-1}=s_0$
. However, this holds true as an immediate consequence of Equation (2-6) with
$s_{m-1,n-1}=s_0 s_{n} s_0^{-1}=s_0$
. However, this holds true as an immediate consequence of Equation (2-6) with
![]() $i=m-1$
.
$i=m-1$
.
Proof of Proposition 2.16
The proof is by induction on
![]() $\ell $
. The case
$\ell $
. The case
![]() $\ell =0$
was treated in Lemma 2.17. Assume that the claimed formulas hold true for some
$\ell =0$
was treated in Lemma 2.17. Assume that the claimed formulas hold true for some
![]() $0\leq \ell \leq m-2$
.
$0\leq \ell \leq m-2$
.
We show that the claimed relations hold true for
![]() $\ell +1$
by induction on p as in Lemma 2.17. Equation (2-4) (with
$\ell +1$
by induction on p as in Lemma 2.17. Equation (2-4) (with
![]() $i=m-2-\ell $
) yields
$i=m-2-\ell $
) yields
from which, by induction (on
![]() $\ell $
), we get
$\ell $
), we get
 $$ \begin{align*} u_{m-2-\ell,1}&=s_{m-1-\ell,0}s_{m-1-\ell,1}^{-1}=(s_0 s_1 \cdots s_{\ell} s_{\ell+1} s_{\ell}^{-1} \cdots s_0^{-1})(s_0 s_1 \cdots s_{\ell} s_{\ell+2}^{-1} s_{\ell}^{-1} \cdots s_0^{-1})\\&=s_0 s_1 \cdots s_{\ell} s_{\ell+1} s_{\ell+2}^{-1} s_{\ell}^{-1} \cdots s_0^{-1}.\end{align*} $$
$$ \begin{align*} u_{m-2-\ell,1}&=s_{m-1-\ell,0}s_{m-1-\ell,1}^{-1}=(s_0 s_1 \cdots s_{\ell} s_{\ell+1} s_{\ell}^{-1} \cdots s_0^{-1})(s_0 s_1 \cdots s_{\ell} s_{\ell+2}^{-1} s_{\ell}^{-1} \cdots s_0^{-1})\\&=s_0 s_1 \cdots s_{\ell} s_{\ell+1} s_{\ell+2}^{-1} s_{\ell}^{-1} \cdots s_0^{-1}.\end{align*} $$
Using this together with Equation (2-8) again, we get also by induction (on
![]() $\ell $
) that
$\ell $
) that
 $$ \begin{align*} s_{m-2-\ell,0}&=s_{m-1-\ell,0}u_{m-2-\ell,1}^{-1}\\ &=(s_0 s_1 \cdots s_{\ell} s_{\ell+1} s_{\ell}^{-1} \cdots s_0^{-1})(s_0 s_1 \cdots s_{\ell} s_{\ell+2} s_{\ell+1}^{-1} s_{\ell}^{-1} \cdots s_0^{-1})\\ &=s_0 s_1 \cdots s_{\ell} s_{\ell+1} s_{\ell+2} s_{\ell+1}^{-1} s_{\ell}^{-1} \cdots s_0^{-1}. \end{align*} $$
$$ \begin{align*} s_{m-2-\ell,0}&=s_{m-1-\ell,0}u_{m-2-\ell,1}^{-1}\\ &=(s_0 s_1 \cdots s_{\ell} s_{\ell+1} s_{\ell}^{-1} \cdots s_0^{-1})(s_0 s_1 \cdots s_{\ell} s_{\ell+2} s_{\ell+1}^{-1} s_{\ell}^{-1} \cdots s_0^{-1})\\ &=s_0 s_1 \cdots s_{\ell} s_{\ell+1} s_{\ell+2} s_{\ell+1}^{-1} s_{\ell}^{-1} \cdots s_0^{-1}. \end{align*} $$
Hence, the statement holds true for
![]() $p=1$
.
$p=1$
.
Assume that the result holds true for some
![]() $1\leq p \leq n-2$
. Equation (2-5) (with
$1\leq p \leq n-2$
. Equation (2-5) (with
![]() ${j=p+1}$
and
${j=p+1}$
and
![]() $i=m-2-\ell $
) yields
$i=m-2-\ell $
) yields
from which by induction (on
![]() $\ell $
and p), we get
$\ell $
and p), we get
 $$ \begin{align*} u_{m-2-\ell,p+1}&=u_{m-2-\ell,p} s_{m-1-\ell,p}s_{m-1-\ell,p+1}^{-1}\\ &= (s_0 s_1 \cdots s_{\ell+1} s_{p+\ell+1}^{-1} s_{\ell}^{-1} s_{\ell-1}^{-1} \cdots s_0^{-1})(s_0 s_1 \cdots s_{\ell} s_{p+\ell+1} s_{\ell}^{-1} s_{\ell-1}^{-1} \cdots s_0^{-1})\\ &~~~~\cdot (s_0 s_1 \cdots s_{\ell} s_{p+\ell+2}^{-1} s_{\ell}^{-1} s_{\ell-1}^{-1} \cdots s_0^{-1})\\ &=s_0 s_1 \cdots s_{\ell+1}s_{p+\ell+2}^{-1} s_{\ell}^{-1} s_{\ell-1}^{-1} \cdots s_0^{-1}. \end{align*} $$
$$ \begin{align*} u_{m-2-\ell,p+1}&=u_{m-2-\ell,p} s_{m-1-\ell,p}s_{m-1-\ell,p+1}^{-1}\\ &= (s_0 s_1 \cdots s_{\ell+1} s_{p+\ell+1}^{-1} s_{\ell}^{-1} s_{\ell-1}^{-1} \cdots s_0^{-1})(s_0 s_1 \cdots s_{\ell} s_{p+\ell+1} s_{\ell}^{-1} s_{\ell-1}^{-1} \cdots s_0^{-1})\\ &~~~~\cdot (s_0 s_1 \cdots s_{\ell} s_{p+\ell+2}^{-1} s_{\ell}^{-1} s_{\ell-1}^{-1} \cdots s_0^{-1})\\ &=s_0 s_1 \cdots s_{\ell+1}s_{p+\ell+2}^{-1} s_{\ell}^{-1} s_{\ell-1}^{-1} \cdots s_0^{-1}. \end{align*} $$
Using this together with Equation (2-9) again, we get also by induction (on
![]() $\ell $
and p) that
$\ell $
and p) that
 $$ \begin{align*} s_{m-2-\ell,p}&=u_{m-2-\ell,p} s_{m-1-\ell,p}u_{m-2-\ell,p+1}^{-1}\\ &= (s_0 s_1 \cdots s_{\ell+1} s_{p+\ell+1}^{-1} s_{\ell}^{-1} s_{\ell-1}^{-1} \cdots s_0^{-1})(s_0 s_1 \cdots s_{\ell} s_{p+\ell+1} s_{\ell}^{-1} s_{\ell-1}^{-1} \cdots s_0^{-1})\\ &~~~~\cdot (s_0 s_1 \cdots s_{\ell}s_{p+\ell+2} s_{\ell+1}^{-1}s_{\ell}^{-1} \cdots s_0^{-1})\\ &=s_0 s_1 \cdots s_{\ell+1}s_{p+\ell+2} s_{\ell+1}^{-1}s_{\ell}^{-1} s_{\ell-1}^{-1} \cdots s_0^{-1},\end{align*} $$
$$ \begin{align*} s_{m-2-\ell,p}&=u_{m-2-\ell,p} s_{m-1-\ell,p}u_{m-2-\ell,p+1}^{-1}\\ &= (s_0 s_1 \cdots s_{\ell+1} s_{p+\ell+1}^{-1} s_{\ell}^{-1} s_{\ell-1}^{-1} \cdots s_0^{-1})(s_0 s_1 \cdots s_{\ell} s_{p+\ell+1} s_{\ell}^{-1} s_{\ell-1}^{-1} \cdots s_0^{-1})\\ &~~~~\cdot (s_0 s_1 \cdots s_{\ell}s_{p+\ell+2} s_{\ell+1}^{-1}s_{\ell}^{-1} \cdots s_0^{-1})\\ &=s_0 s_1 \cdots s_{\ell+1}s_{p+\ell+2} s_{\ell+1}^{-1}s_{\ell}^{-1} s_{\ell-1}^{-1} \cdots s_0^{-1},\end{align*} $$
and hence both statements also hold true for
![]() $p+1$
. Therefore, the result holds true at level
$p+1$
. Therefore, the result holds true at level
![]() $\ell +1$
for all
$\ell +1$
for all
![]() $1\leq p \leq n-1$
and it remains to check the first statement (at level
$1\leq p \leq n-1$
and it remains to check the first statement (at level
![]() $\ell +1$
) for
$\ell +1$
) for
![]() $p=n$
, that is, that
$p=n$
, that is, that
To this end, we use Equation (2-6) with
![]() $i=m-2-\ell $
, that is,
$i=m-2-\ell $
, that is,
However, we already know by induction (on
![]() $\ell $
) that
$\ell $
) that
![]() $s_{m-1-\ell ,0}=s_0 s_1 \cdots s_{\ell +1} s_{\ell }^{-1} \cdots s_0^{-1}$
(alternatively both factors in the product
$s_{m-1-\ell ,0}=s_0 s_1 \cdots s_{\ell +1} s_{\ell }^{-1} \cdots s_0^{-1}$
(alternatively both factors in the product
![]() $u_{m-2-\ell ,n-1} s_{m-1-\ell ,n-1}$
are also already known, and multiplying them yields the same result).
$u_{m-2-\ell ,n-1} s_{m-1-\ell ,n-1}$
are also already known, and multiplying them yields the same result).
Setting
![]() $\ell =m-1$
in the first item of Proposition 2.16, we get
$\ell =m-1$
in the first item of Proposition 2.16, we get
Lemma 2.18. Setting
![]() $x_i=s_{i-1}$
for all
$x_i=s_{i-1}$
for all
![]() $1\leq i \leq n$
, the set of relations (2-10) is equivalent to the second set of relations in the statement of Theorem 2.12, that is, to
$1\leq i \leq n$
, the set of relations (2-10) is equivalent to the second set of relations in the statement of Theorem 2.12, that is, to
Proof. The set of relations in Equation (2-10) can be rewritten as
We show that they imply the relations
![]() $x_1 x_2 \cdots x_m = x_j x_{j+1} \cdots x_{j+m-1} ~\text { for all } j=2, \ldots , n$
, by induction on j. Putting
$x_1 x_2 \cdots x_m = x_j x_{j+1} \cdots x_{j+m-1} ~\text { for all } j=2, \ldots , n$
, by induction on j. Putting
![]() $i=1$
in Equation (2-11) and canceling
$i=1$
in Equation (2-11) and canceling
![]() $x_1$
, we get the relation
$x_1$
, we get the relation
![]() $x_1 x_2\ldots x_m= x_2 x_3\cdots x_{m+1}$
, which proves the case
$x_1 x_2\ldots x_m= x_2 x_3\cdots x_{m+1}$
, which proves the case
![]() $j=2$
. Assume that
$j=2$
. Assume that
![]() $x_1 x_2 \cdots x_m = x_j x_{j+1} \cdots x_{j+m-1}$
for some
$x_1 x_2 \cdots x_m = x_j x_{j+1} \cdots x_{j+m-1}$
for some
![]() $2\leq j < n$
. From Equation (2-11) and by induction, we get
$2\leq j < n$
. From Equation (2-11) and by induction, we get
Canceling
![]() $x_j$
on both sides yields
$x_j$
on both sides yields
![]() $x_1 x_2 \cdots x_m=x_{j+1}\cdots x_{j+m-1} x_{j+m}$
. Hence, the relations in Equation (2-10) imply the second set of relations.
$x_1 x_2 \cdots x_m=x_{j+1}\cdots x_{j+m-1} x_{j+m}$
. Hence, the relations in Equation (2-10) imply the second set of relations.
Conversely, if the second set of relations holds true, then for all
![]() $1 \leq i \leq n$
, we have
$1 \leq i \leq n$
, we have
which concludes the proof.
End of the proof of Theorem 2.12
It follows from Proposition 2.16 that the elements
![]() $x_i$
terms generate H. Lemma 2.18 shows that the second set of relations in the statement of Theorem 2.12 holds true in H. We also know that the first set of relations holds true as a consequence of Relations (2-2). To conclude the proof of Theorem 2.12, it therefore remains to show that, replacing the various
$x_i$
terms generate H. Lemma 2.18 shows that the second set of relations in the statement of Theorem 2.12 holds true in H. We also know that the first set of relations holds true as a consequence of Relations (2-2). To conclude the proof of Theorem 2.12, it therefore remains to show that, replacing the various
![]() $u_{i,j}$
and
$u_{i,j}$
and
![]() $s_{i,j}$
in Relations (2-4)–(2-6) by their expressions in terms of
$s_{i,j}$
in Relations (2-4)–(2-6) by their expressions in terms of
![]() $s_0, s_1, \ldots , s_{n-1}$
obtained in Proposition 2.16, we get no other relations than those in the statement of Theorem 2.12.
$s_0, s_1, \ldots , s_{n-1}$
obtained in Proposition 2.16, we get no other relations than those in the statement of Theorem 2.12.
This is a direct check. For Relations (2-2), as by Proposition 2.16, every
![]() $s_{i,j}$
is conjugate to some
$s_{i,j}$
is conjugate to some
![]() $s_i$
, we get that Relations (2-2) follows from the relations
$s_i$
, we get that Relations (2-2) follows from the relations
![]() $x_i^k=1$
for all
$x_i^k=1$
for all
![]() $1\leq i \leq n$
. We now consider Relations (2-3). These relations tell us that
$1\leq i \leq n$
. We now consider Relations (2-3). These relations tell us that
![]() $\text { for all } i\in \{0, \ldots , m-1\}, j\in \{1, \ldots , n-1\}$
, we have
$\text { for all } i\in \{0, \ldots , m-1\}, j\in \{1, \ldots , n-1\}$
, we have
![]() $\prod _{q=i}^{i+m-1} u_{q,j}=1$
. We separate this product as
$\prod _{q=i}^{i+m-1} u_{q,j}=1$
. We separate this product as
![]() $\prod _{q=i}^{m-1} u_{q,j} \prod _{q=m}^{m-1+i} u_{q,j}$
. Proposition 2.16 yields
$\prod _{q=i}^{m-1} u_{q,j} \prod _{q=m}^{m-1+i} u_{q,j}$
. Proposition 2.16 yields
 $$ \begin{align*} \prod_{q=i}^{m-1} u_{q,j} &=\prod_{q=i}^{m-1} s_0 s_1 \cdots s_{m-1-q} s_{j+m-1-q}^{-1} s_{m-2-q}^{-1} s_{m-3-q}^{-1} \cdots s_0^{-1} \\& =s_0 s_1 \cdots s_{m-1-i} s_{j+m-1-i}^{-1} s_{j+m-2-i}^{-1} \cdots s_{j}^{-1},\end{align*} $$
$$ \begin{align*} \prod_{q=i}^{m-1} u_{q,j} &=\prod_{q=i}^{m-1} s_0 s_1 \cdots s_{m-1-q} s_{j+m-1-q}^{-1} s_{m-2-q}^{-1} s_{m-3-q}^{-1} \cdots s_0^{-1} \\& =s_0 s_1 \cdots s_{m-1-i} s_{j+m-1-i}^{-1} s_{j+m-2-i}^{-1} \cdots s_{j}^{-1},\end{align*} $$
while
 $$ \begin{align*} \prod_{q=m}^{m-1+i} u_{q,j}&=\prod_{q=0}^{i-1} u_{q,j}=\prod_{q=0}^{i-1} s_0 s_1 \cdots s_{m-1-q} s_{j+m-1-q}^{-1} s_{m-2-q}^{-1} s_{m-3-q}^{-1} \cdots s_0^{-1}\\ &=s_0 s_1 \cdots s_{m-1} s_{j+m-1}^{-1}s_{j+m-2}^{-1}\cdots s_{j+m-i}^{-1} s_{m-i-1}^{-1} s_{m-i-2}^{-1}\cdots s_0^{-1}.\end{align*} $$
$$ \begin{align*} \prod_{q=m}^{m-1+i} u_{q,j}&=\prod_{q=0}^{i-1} u_{q,j}=\prod_{q=0}^{i-1} s_0 s_1 \cdots s_{m-1-q} s_{j+m-1-q}^{-1} s_{m-2-q}^{-1} s_{m-3-q}^{-1} \cdots s_0^{-1}\\ &=s_0 s_1 \cdots s_{m-1} s_{j+m-1}^{-1}s_{j+m-2}^{-1}\cdots s_{j+m-i}^{-1} s_{m-i-1}^{-1} s_{m-i-2}^{-1}\cdots s_0^{-1}.\end{align*} $$
Now we have the relation
![]() $\prod _{q=i}^{m-1} u_{q,j} \prod _{q=m}^{m-1+i} u_{q,j}=1$
. Replacing the expressions obtained above and conjugating by
$\prod _{q=i}^{m-1} u_{q,j} \prod _{q=m}^{m-1+i} u_{q,j}=1$
. Replacing the expressions obtained above and conjugating by
![]() $(s_0 s_1 \cdots s_{m-1-i})^{-1}$
, we get the relation
$(s_0 s_1 \cdots s_{m-1-i})^{-1}$
, we get the relation
Putting the inverses in the right-hand side and replacing
![]() $s_{i-1}$
by
$s_{i-1}$
by
![]() $x_i$
for all i, we get the equivalent relation
$x_i$
for all i, we get the equivalent relation
![]() $x_1 x_2 \cdots x_m=x_{j+1} x_{j+2} \cdots x_{j+m},$
which we already obtained in Lemma 2.18.
$x_1 x_2 \cdots x_m=x_{j+1} x_{j+2} \cdots x_{j+m},$
which we already obtained in Lemma 2.18.
Hence, Relations (2-2) and (2-3) yield no new relations in H. We need to check that the same holds true for the remaining Equations (2-4)–(2-6). We check it for Equation (2-4). For any
![]() $0\leq i \leq m-1$
, we have
$0\leq i \leq m-1$
, we have
 $$ \begin{align*} s_{i,0} u_{i,1}&=(s_0 s_1 \cdots s_{m-1-i} s_{m-i} s_{m-1-i}^{-1} \cdots s_0^{-1})(s_0 s_1 \cdots s_{m-1-i} s_{m-i}^{-1} s_{m-2-i}^{-1} \cdots s_0^{-1})\\ &=s_0 s_1 \cdots s_{m-1-i}s_{m-2-i}^{-1} \cdots s_0^{-1},\end{align*} $$
$$ \begin{align*} s_{i,0} u_{i,1}&=(s_0 s_1 \cdots s_{m-1-i} s_{m-i} s_{m-1-i}^{-1} \cdots s_0^{-1})(s_0 s_1 \cdots s_{m-1-i} s_{m-i}^{-1} s_{m-2-i}^{-1} \cdots s_0^{-1})\\ &=s_0 s_1 \cdots s_{m-1-i}s_{m-2-i}^{-1} \cdots s_0^{-1},\end{align*} $$
 $$ \begin{align*} u_{i,1} s_{i+1,1}&=(s_0 s_1 \cdots s_{m-1-i} s_{m-i}^{-1} s_{m-2-i}^{-1} \cdots s_0^{-1})(s_0 s_1 \cdots s_{m-i-2} s_{m-i} s_{m-i-2}^{-1} \cdots s_0^{-1})\\ &=s_0 s_1 \cdots s_{m-1-i}s_{m-2-i}^{-1} \cdots s_0^{-1},\end{align*} $$
$$ \begin{align*} u_{i,1} s_{i+1,1}&=(s_0 s_1 \cdots s_{m-1-i} s_{m-i}^{-1} s_{m-2-i}^{-1} \cdots s_0^{-1})(s_0 s_1 \cdots s_{m-i-2} s_{m-i} s_{m-i-2}^{-1} \cdots s_0^{-1})\\ &=s_0 s_1 \cdots s_{m-1-i}s_{m-2-i}^{-1} \cdots s_0^{-1},\end{align*} $$
and we thus see that both
![]() $s_{i,0} u_{i,1}$
and
$s_{i,0} u_{i,1}$
and
![]() $u_{i,1} s_{i+1,1}$
yield the same words, and by Proposition 2.16, they are also equal to a word for
$u_{i,1} s_{i+1,1}$
yield the same words, and by Proposition 2.16, they are also equal to a word for
![]() $s_{i+1,0}$
. We only deleted factors of the form
$s_{i+1,0}$
. We only deleted factors of the form
![]() $xx^{-1}$
to obtain these equalities, and hence these relations do not yield any relation in H at all.
$xx^{-1}$
to obtain these equalities, and hence these relations do not yield any relation in H at all.
It is checked that Equations (2-5) and (2-6) do not give any new relations in H in the exact same way as we did for Equation (2-4) above. For Equation (2-5), replacing the various factors using Proposition 2.16 and deleting
![]() $xx^{-1}$
factors as above, one sees that
$xx^{-1}$
factors as above, one sees that
![]() $s_{i,j-1} u_{i,j}$
,
$s_{i,j-1} u_{i,j}$
,
![]() $u_{i,j} s_{i+1,j}$
, and
$u_{i,j} s_{i+1,j}$
, and
![]() $u_{i,j-1}s_{i+1,j-1}$
again yield the same words, equal to the word for
$u_{i,j-1}s_{i+1,j-1}$
again yield the same words, equal to the word for
![]() $s_{i+1,0}$
obtained in Proposition 2.16. For Equation (2-6), we also get that
$s_{i+1,0}$
obtained in Proposition 2.16. For Equation (2-6), we also get that
![]() $s_{i,n-1}$
and
$s_{i,n-1}$
and
![]() $u_{i,n-1} s_{i+1,n-1}$
yield the same words, also equal to the word for
$u_{i,n-1} s_{i+1,n-1}$
yield the same words, also equal to the word for
![]() $s_{i+1,0}$
obtained in Proposition 2.16.
$s_{i+1,0}$
obtained in Proposition 2.16.
The last statement that
![]() $x_i$
corresponds in G to
$x_i$
corresponds in G to
![]() $t^{i-1} s t^{1-i}$
has already been seen in Equation (2-7) above.
$t^{i-1} s t^{1-i}$
has already been seen in Equation (2-7) above.
2.3 Representation by complex reflection groups
Achar and Aubert [Reference Achar and Aubert2, Section 4] constructed a representation of
![]() $G=J(\begin {smallmatrix} a & b & c\\ ~& ~& ~\end {smallmatrix})$
(and hence of any J-group) on
$G=J(\begin {smallmatrix} a & b & c\\ ~& ~& ~\end {smallmatrix})$
(and hence of any J-group) on
![]() $\mathbb {C}^2$
, where the generators
$\mathbb {C}^2$
, where the generators
![]() $s,t$
, and u act by (pseudo-)reflections. This yields reflection representations of J-groups and hence, thanks to Theorem 2.12, of every toric reflection group. As we see in this section, this representation is not faithful in general when
$s,t$
, and u act by (pseudo-)reflections. This yields reflection representations of J-groups and hence, thanks to Theorem 2.12, of every toric reflection group. As we see in this section, this representation is not faithful in general when
![]() $W(k,n,m)$
is infinite.
$W(k,n,m)$
is infinite.
The representation is constructed as follows. Let K be a finite abelian extension of
![]() $\mathbb {Q}$
containing the roots of unity of orders
$\mathbb {Q}$
containing the roots of unity of orders
![]() $2a, 2b,$
and
$2a, 2b,$
and
![]() $2c$
. Let
$2c$
. Let
![]() $\mathbb {Z}_{K}$
be the ring of algebraic integers of K. Let
$\mathbb {Z}_{K}$
be the ring of algebraic integers of K. Let
![]() $\theta =e^{i\pi /a}$
,
$\theta =e^{i\pi /a}$
,
![]() $\phi =e^{i\pi /b}$
, and
$\phi =e^{i\pi /b}$
, and
![]() $\psi =e^{i\pi /c}$
. Choose two elements
$\psi =e^{i\pi /c}$
. Choose two elements
![]() $q,r\in \mathbb {Z}_K$
such that
$q,r\in \mathbb {Z}_K$
such that
![]() $qr=\theta \phi (\psi +\psi ^{-1})-\theta ^2-\phi ^2$
. Then setting
$qr=\theta \phi (\psi +\psi ^{-1})-\theta ^2-\phi ^2$
. Then setting
 $$ \begin{align*} \rho(s)=\begin{pmatrix} \theta^2 & q \\ 0 & 1\end{pmatrix},\quad \rho(t)=\begin{pmatrix} 1 & 0\\ r & \phi^2 \end{pmatrix},\quad \rho(u)=\theta \phi\psi \rho(t)^{-1} \rho(s)^{-1}, \end{align*} $$
$$ \begin{align*} \rho(s)=\begin{pmatrix} \theta^2 & q \\ 0 & 1\end{pmatrix},\quad \rho(t)=\begin{pmatrix} 1 & 0\\ r & \phi^2 \end{pmatrix},\quad \rho(u)=\theta \phi\psi \rho(t)^{-1} \rho(s)^{-1}, \end{align*} $$
we have the following proposition.
Proposition 2.19 [Reference Achar and Aubert2, Proposition 4.2]
The map
![]() $\rho $
extends to a group homomorphism
$\rho $
extends to a group homomorphism
![]() $G\longrightarrow \mathrm {GL}_2(K)$
.
$G\longrightarrow \mathrm {GL}_2(K)$
.
The following example shows that
![]() $\rho $
is unfaithful in general when
$\rho $
is unfaithful in general when
![]() $W(k,n,m)$
is infinite.
$W(k,n,m)$
is infinite.
Example 2.20. Let
![]() $k=6, n=2, m=3$
. By Theorem 2.12, the group
$k=6, n=2, m=3$
. By Theorem 2.12, the group
![]() $W(6,2,3)$
can be identified with the subgroup of
$W(6,2,3)$
can be identified with the subgroup of
![]() $G=J(\begin {smallmatrix} 6 & 2 & 3\\ ~& ~& ~\end {smallmatrix})$
generated by
$G=J(\begin {smallmatrix} 6 & 2 & 3\\ ~& ~& ~\end {smallmatrix})$
generated by
![]() $x_1=s$
and
$x_1=s$
and
![]() $x_2=tst^{-1}=tst$
. Note that, thanks to Theorem 2.12, it is a quotient of the
$x_2=tst^{-1}=tst$
. Note that, thanks to Theorem 2.12, it is a quotient of the
![]() $3$
-strand braid group
$3$
-strand braid group
by the relations
![]() $x_1^6=1=x_2^6$
, studied by Coxeter in [Reference Coxeter15]. By definition of
$x_1^6=1=x_2^6$
, studied by Coxeter in [Reference Coxeter15]. By definition of
![]() $\rho (u)$
and since
$\rho (u)$
and since
![]() $stu=tus=ust$
, we have that
$stu=tus=ust$
, we have that
![]() $\rho (s)\rho (t)\rho (u)$
is the scalar matrix
$\rho (s)\rho (t)\rho (u)$
is the scalar matrix
![]() $\theta \phi \psi \mathrm {Id}$
, which in this case is
$\theta \phi \psi \mathrm {Id}$
, which in this case is
![]() $-\mathrm {Id}$
. It implies that
$-\mathrm {Id}$
. It implies that
![]() $\rho (stu)$
has order
$\rho (stu)$
has order
![]() $2$
. Now since
$2$
. Now since
![]() $stu$
is central in G and u has order
$stu$
is central in G and u has order
![]() $6$
, we have that
$6$
, we have that
![]() $(stu)^6=(stuu^{-1})^6=(st)^6$
, from which we deduce that
$(stu)^6=(stuu^{-1})^6=(st)^6$
, from which we deduce that
However, there is a surjective map
![]() $W(6,2,3)\twoheadrightarrow W(3,2,3)$
,
$W(6,2,3)\twoheadrightarrow W(3,2,3)$
,
![]() $x_i\mapsto x_i$
. The group
$x_i\mapsto x_i$
. The group
![]() $W(3,2,3)$
is the complex reflection group
$W(3,2,3)$
is the complex reflection group
![]() $G_4$
, and one checks that
$G_4$
, and one checks that
![]() $x_1 x_2$
has order
$x_1 x_2$
has order
![]() $6$
in this group. It follows that
$6$
in this group. It follows that
![]() $(x_1 x_2)^3$
cannot be equal to
$(x_1 x_2)^3$
cannot be equal to
![]() $1$
in
$1$
in
![]() $W(6,2,3)$
, and that Achar and Aubert’s representation is unfaithful in this case. The same observation can be made with the representation constructed by Coxeter in [Reference Coxeter15, Section 7].
$W(6,2,3)$
, and that Achar and Aubert’s representation is unfaithful in this case. The same observation can be made with the representation constructed by Coxeter in [Reference Coxeter15, Section 7].
Moreover, the isomorphism class of the representation depends in fact on the choice of q and r. In the above case, we have
![]() $qr=0$
. Choosing
$qr=0$
. Choosing
![]() $q=0=r$
yields matrices
$q=0=r$
yields matrices
![]() $\rho (s)$
and
$\rho (s)$
and
![]() $\rho (t)$
commuting with each other, while choosing
$\rho (t)$
commuting with each other, while choosing
![]() $q=1, r=0$
yields matrices
$q=1, r=0$
yields matrices
![]() $\rho (s)$
and
$\rho (s)$
and
![]() $\rho (t)$
which do not commute with each other.
$\rho (t)$
which do not commute with each other.
The above example raises the following questions.
Question 2.21. Are there examples of infinite toric reflection groups for which Achar and Aubert’s representation is faithful? For which toric reflection groups
![]() $W(k,n,m)$
is there a (canonical) faithful representation as a complex reflection group?
$W(k,n,m)$
is there a (canonical) faithful representation as a complex reflection group?
3 Center of toric reflection groups
The aim of this section is to establish that toric reflection groups have a cyclic center, and to show that the quotient by their center is an alternating subgroup of a Coxeter group of rank three. This is a key ingredient for the classification of toric reflection groups that we give in the next section. We assume the reader is familiar with the general theory of Coxeter groups and their parabolic subgroups (see for instance [Reference Abramenko and Brown1, Reference Bourbaki8] for basics on the topic).
Let us introduce some notation and properties of Coxeter groups that are used in the next sections. We denote by
![]() $(W,S)$
a Coxeter system, with S finite. Recall that for
$(W,S)$
a Coxeter system, with S finite. Recall that for
![]() $I\subseteq S$
, the subgroup
$I\subseteq S$
, the subgroup
![]() $W_I:=\langle s~|~s\in I \rangle $
is called a standard parabolic subgroup of W, and that the pair
$W_I:=\langle s~|~s\in I \rangle $
is called a standard parabolic subgroup of W, and that the pair
![]() $(W_I, I)$
is itself a Coxeter system. These subgroups have particularly nice properties: for instance, any S-reduced decomposition of an element
$(W_I, I)$
is itself a Coxeter system. These subgroups have particularly nice properties: for instance, any S-reduced decomposition of an element
![]() $w\in W$
that lies in
$w\in W$
that lies in
![]() $W_I$
has all its letters in I—see [Reference Abramenko and Brown1, Section 2.3.2]. A subgroup of the form
$W_I$
has all its letters in I—see [Reference Abramenko and Brown1, Section 2.3.2]. A subgroup of the form
![]() $x W_I x^{-1}$
of W, where
$x W_I x^{-1}$
of W, where
![]() $I\subseteq S$
and
$I\subseteq S$
and
![]() $x\in W$
, is called a parabolic subgroup of W.
$x\in W$
, is called a parabolic subgroup of W.
More generally, one can show that any subgroup
![]() $W'$
of W generated by a subset of the set
$W'$
of W generated by a subset of the set
![]() $T=\bigcup _{w\in W} w S w^{-1}$
of reflections of W is itself a Coxeter group in a canonical way—see [Reference Dyer18]. Such a subgroup is called a reflection subgroup of W.
$T=\bigcup _{w\in W} w S w^{-1}$
of reflections of W is itself a Coxeter group in a canonical way—see [Reference Dyer18]. Such a subgroup is called a reflection subgroup of W.
Given a Coxeter group W with length function
![]() $\ell _S$
with respect to the generating set S, the subset
$\ell _S$
with respect to the generating set S, the subset
![]() $W^+$
of elements w such that
$W^+$
of elements w such that
![]() $\ell _S(w)$
is even forms a subgroup of index two of W (hence normal), called the alternating subgroup of W, which we denote
$\ell _S(w)$
is even forms a subgroup of index two of W (hence normal), called the alternating subgroup of W, which we denote
![]() $W^+$
.
$W^+$
.
3.1 Center of alternating subgroups of Coxeter groups
We need the following result, which applies to an arbitrary Coxeter group of rank at least
![]() $3$
, though we only apply it in the rank three case. Recall that the center of an infinite and irreducible Coxeter group is trivial (see [Reference Bourbaki8, Ch. V, Section 4, Exercise 3]).
$3$
, though we only apply it in the rank three case. Recall that the center of an infinite and irreducible Coxeter group is trivial (see [Reference Bourbaki8, Ch. V, Section 4, Exercise 3]).
Proposition 3.1 (Center of alternating subgroups of Coxeter groups)
Let
![]() $(W,S)$
be a Coxeter system with
$(W,S)$
be a Coxeter system with
![]() $|S| \geq 3$
. Let
$|S| \geq 3$
. Let
![]() $W^+$
be the alternating subgroup of W. Then
$W^+$
be the alternating subgroup of W. Then
![]() ${Z(W^+)\subseteq Z(W)}$
. In particular, as infinite and irreducible Coxeter groups have trivial centers, the center of the alternating subgroup of an infinite and irreducible Coxeter group of rank at least three is trivial.
${Z(W^+)\subseteq Z(W)}$
. In particular, as infinite and irreducible Coxeter groups have trivial centers, the center of the alternating subgroup of an infinite and irreducible Coxeter group of rank at least three is trivial.
Proof. Let
![]() $x\in Z(W^+)$
. Let T denote the set
$x\in Z(W^+)$
. Let T denote the set
![]() $\bigcup _{w\in W} w S w^{-1}$
of reflections of W. For every
$\bigcup _{w\in W} w S w^{-1}$
of reflections of W. For every
![]() $s\in S$
, define
$s\in S$
, define
![]() $s':=xsx^{-1}\in T$
. We show that
$s':=xsx^{-1}\in T$
. We show that
![]() $s'=s$
for all
$s'=s$
for all
![]() $s\in S$
, which concludes the proof.
$s\in S$
, which concludes the proof.
Let
![]() $s,t\in S$
with
$s,t\in S$
with
![]() $s\neq t$
. As x is central in
$s\neq t$
. As x is central in
![]() $W^+$
, we have
$W^+$
, we have
![]() $xst=stx$
. We also have
$xst=stx$
. We also have
![]() $xst=s't'x$
, which yields
$xst=s't'x$
, which yields
![]() $st=s't'$
. By [Reference Dyer19, Lemma 3.1], the reflection subgroup
$st=s't'$
. By [Reference Dyer19, Lemma 3.1], the reflection subgroup
![]() ${W':=\langle s,t,s',t'\rangle }$
of W is dihedral. We claim that
${W':=\langle s,t,s',t'\rangle }$
of W is dihedral. We claim that
![]() $W'$
is the standard parabolic subgroup generated by s and t. Indeed, writing
$W'$
is the standard parabolic subgroup generated by s and t. Indeed, writing
![]() $\chi (W')$
for its set of canonical generators as a Coxeter group (see [Reference Dyer18]), we have
$\chi (W')$
for its set of canonical generators as a Coxeter group (see [Reference Dyer18]), we have
![]() $|\chi (W')|=2$
and
$|\chi (W')|=2$
and
![]() $s,t\in \chi (W')$
since
$s,t\in \chi (W')$
since
![]() $s,t\in S$
, and hence
$s,t\in S$
, and hence
![]() $W'=\langle s, t\rangle $
. In particular, we have
$W'=\langle s, t\rangle $
. In particular, we have
![]() $s',t'\in \langle s, t\rangle $
. Assume that
$s',t'\in \langle s, t\rangle $
. Assume that
![]() $s'\neq s$
. Then since
$s'\neq s$
. Then since
![]() $s'\in \langle s,t\rangle $
and
$s'\in \langle s,t\rangle $
and
![]() $\langle s, t\rangle $
is a standard parabolic subgroup of W, the reflection
$\langle s, t\rangle $
is a standard parabolic subgroup of W, the reflection
![]() $s'$
has a reduced S-decomposition (equivalently all reduced S-decompositions) in which t has to appear. Now, since W has rank at least
$s'$
has a reduced S-decomposition (equivalently all reduced S-decompositions) in which t has to appear. Now, since W has rank at least
![]() $3$
, let
$3$
, let
![]() $r\in S\backslash \{s,t\}$
. Arguing as above, we have
$r\in S\backslash \{s,t\}$
. Arguing as above, we have
![]() $sr=s'r'$
and
$sr=s'r'$
and
![]() $s'\in \langle s,r\rangle $
. This is a contradiction, as t appears in reduced S-decompositions of
$s'\in \langle s,r\rangle $
. This is a contradiction, as t appears in reduced S-decompositions of
![]() $s'$
, while all elements in
$s'$
, while all elements in
![]() $\langle s, r\rangle $
have all their S-reduced decompositions only involving the letters s and r. Hence,
$\langle s, r\rangle $
have all their S-reduced decompositions only involving the letters s and r. Hence,
![]() $s=s'$
.
$s=s'$
.
The above result is not valid for irreducible Coxeter groups of rank two: let
![]() ${W=I_2(m)}$
be the dihedral group of order
${W=I_2(m)}$
be the dihedral group of order
![]() $2m$
(
$2m$
(
![]() $m\geq 3$
). Then
$m\geq 3$
). Then
![]() $W^+\cong C_m$
, the cyclic group of order m. It is the rotation subgroup of W. Hence,
$W^+\cong C_m$
, the cyclic group of order m. It is the rotation subgroup of W. Hence,
![]() $W^+=Z(W^+)$
, while
$W^+=Z(W^+)$
, while
![]() $Z(W)$
is trivial for odd m and isomorphic to
$Z(W)$
is trivial for odd m and isomorphic to
![]() $C_2$
for even m. The infinite dihedral group W has trivial center, while
$C_2$
for even m. The infinite dihedral group W has trivial center, while
![]() $W^+\cong \mathbb {Z}$
.
$W^+\cong \mathbb {Z}$
.
Also note that it has been shown that for irreducible, infinite, and nonaffine Coxeter groups, the center of any finite index subgroup is trivial (see [Reference Paris27, Proposition 6.4] or [Reference Qi28]).
3.2 Center of toric reflection groups and their parent J-groups
Let
![]() $k,n,m\geq 2$
with
$k,n,m\geq 2$
with
![]() $n<m$
, and n and m coprime. The aim of this section is to show that the center of a toric reflection group is cyclic. A step to achieve this is to show that
$n<m$
, and n and m coprime. The aim of this section is to show that the center of a toric reflection group is cyclic. A step to achieve this is to show that
![]() $W(k,n,m)/ Z(W(k,n,m))$
is isomorphic to the alternating subgroup
$W(k,n,m)/ Z(W(k,n,m))$
is isomorphic to the alternating subgroup
![]() $W_{k,n,m}^+$
of the rank-three Coxeter group
$W_{k,n,m}^+$
of the rank-three Coxeter group
 $$ \begin{align*} W_{k,n,m}=\bigg\langle r_1,r_2,r_3 \ \bigg\vert\ \begin{matrix} r_1^2=r_2^2=r_3^2=1,\\ (r_1 r_2)^k=(r_2 r_3)^n=(r_3 r_1)^m=1. \end{matrix} \ \bigg\rangle \end{align*} $$
$$ \begin{align*} W_{k,n,m}=\bigg\langle r_1,r_2,r_3 \ \bigg\vert\ \begin{matrix} r_1^2=r_2^2=r_3^2=1,\\ (r_1 r_2)^k=(r_2 r_3)^n=(r_3 r_1)^m=1. \end{matrix} \ \bigg\rangle \end{align*} $$
A presentation for the alternating subgroup
![]() $W^+$
of an arbitrary Coxeter group W is given by Bourbaki [Reference Bourbaki8, Ch. IV, Section 1, Exercise 9]. In the specific case of
$W^+$
of an arbitrary Coxeter group W is given by Bourbaki [Reference Bourbaki8, Ch. IV, Section 1, Exercise 9]. In the specific case of
![]() $W_{k,n,m}$
, it yields the presentation
$W_{k,n,m}$
, it yields the presentation
where in terms of the generators
![]() $r_1, r_2, r_3$
of
$r_1, r_2, r_3$
of
![]() $W_{k,n,m}$
, we have
$W_{k,n,m}$
, we have
![]() $a=r_1 r_2$
,
$a=r_1 r_2$
,
![]() $b=r_3 r_2$
(hence,
$b=r_3 r_2$
(hence,
![]() $ba^{-1}=r_3 r_1$
).
$ba^{-1}=r_3 r_1$
).
Lemma 3.2. Let
![]() $m=qn+r$
be the Euclidean division of m by n. Let
$m=qn+r$
be the Euclidean division of m by n. Let
![]() $\delta :=x_1 x_2 \cdots x_m$
. Then, taking indices modulo n, we have
$\delta :=x_1 x_2 \cdots x_m$
. Then, taking indices modulo n, we have
![]() $x_i \delta = \delta x_{i+r}$
for all
$x_i \delta = \delta x_{i+r}$
for all
![]() $i=1, \ldots , n$
.
$i=1, \ldots , n$
.
Proof. As
![]() $m\equiv r ~(\mathrm {mod}~n)$
, using the defining relations of
$m\equiv r ~(\mathrm {mod}~n)$
, using the defining relations of
![]() $W(k,n,m)$
, we have for all
$W(k,n,m)$
, we have for all
![]() $i=1, \ldots , n$
,
$i=1, \ldots , n$
,
Let
![]() $c:=(x_1 x_2 \cdots x_n)^m\in W(k,n,m)$
. Note that we have
$c:=(x_1 x_2 \cdots x_n)^m\in W(k,n,m)$
. Note that we have
![]() $(x_1 x_2 \cdots x_n)^m=(x_1 x_2 \cdots x_m)^n$
. Moreover, by Lemma 3.2, the element c is central in
$(x_1 x_2 \cdots x_n)^m=(x_1 x_2 \cdots x_m)^n$
. Moreover, by Lemma 3.2, the element c is central in
![]() $W(k,n,m)$
as
$W(k,n,m)$
as
We denote by
![]() $\overline {W(k,n,m)}$
the quotient of
$\overline {W(k,n,m)}$
the quotient of
![]() $W(k,n,m)$
by the extra relation
$W(k,n,m)$
by the extra relation
![]() $c=1$
.
$c=1$
.
We clearly have a group homomorphism
![]() $J(\begin {smallmatrix} k & n & m \\ ~ & ~ & ~ \end {smallmatrix})\longrightarrow W_{k,n,m}^+$
with
$J(\begin {smallmatrix} k & n & m \\ ~ & ~ & ~ \end {smallmatrix})\longrightarrow W_{k,n,m}^+$
with
![]() ${s\mapsto r_1 r_2}$
,
${s\mapsto r_1 r_2}$
,
![]() ${t\mapsto r_2 r_3}$
,
${t\mapsto r_2 r_3}$
,
![]() ${u\mapsto r_3 r_1}$
. By restriction, it induces a homomorphism
${u\mapsto r_3 r_1}$
. By restriction, it induces a homomorphism
![]() $W(k,n,m)\longrightarrow W_{k,n,m}^+$
. Considering the generators
$W(k,n,m)\longrightarrow W_{k,n,m}^+$
. Considering the generators
![]() $x_i$
of
$x_i$
of
![]() $W(k,n,m)\cong J(\begin {smallmatrix} k & n & m\\ ~& n& m\end {smallmatrix})$
and recalling from Theorem 2.12 that in terms of the generators of the parent J-group
$W(k,n,m)\cong J(\begin {smallmatrix} k & n & m\\ ~& n& m\end {smallmatrix})$
and recalling from Theorem 2.12 that in terms of the generators of the parent J-group
![]() $J(\begin {smallmatrix} k & n & m\\ ~& ~& ~\end {smallmatrix})$
, we have
$J(\begin {smallmatrix} k & n & m\\ ~& ~& ~\end {smallmatrix})$
, we have
![]() $x_i=t^{i-1} s t^{1-i}$
for all
$x_i=t^{i-1} s t^{1-i}$
for all
![]() $i=1, \ldots , n$
, we see that such a homomorphism maps
$i=1, \ldots , n$
, we see that such a homomorphism maps
![]() $x_1 x_2 \cdots x_n$
to
$x_1 x_2 \cdots x_n$
to
![]() $(r_1 r_3)^n$
, which has order m in
$(r_1 r_3)^n$
, which has order m in
![]() $W_{k,n,m}$
: indeed, by the general theory of Coxeter groups, we know that
$W_{k,n,m}$
: indeed, by the general theory of Coxeter groups, we know that
![]() $r_1 r_3$
has order m (see for instance [Reference Abramenko and Brown1, Section 2.3.3]), and n and m are coprime. In particular, the element c is mapped to
$r_1 r_3$
has order m (see for instance [Reference Abramenko and Brown1, Section 2.3.3]), and n and m are coprime. In particular, the element c is mapped to
![]() $1$
; hence the above homomorphism factors through
$1$
; hence the above homomorphism factors through
![]() $\overline {W(k,n,m)}$
, and we denote by
$\overline {W(k,n,m)}$
, and we denote by
![]() $\varphi : \overline {W(k,n,m)}\longrightarrow W_{k,n,m}^+$
the obtained homomorphism.
$\varphi : \overline {W(k,n,m)}\longrightarrow W_{k,n,m}^+$
the obtained homomorphism.
The main result of the section is given by the following statement.
Theorem 3.3 (Center of toric reflection groups)
Let
![]() $G=J(\begin {smallmatrix} k & n & m\\ ~& ~& ~\end {smallmatrix})$
, where
$G=J(\begin {smallmatrix} k & n & m\\ ~& ~& ~\end {smallmatrix})$
, where
![]() $k,n,m\geq 2$
,
$k,n,m\geq 2$
,
![]() $n<m$
, and
$n<m$
, and
![]() $n,m$
are coprime.
$n,m$
are coprime.
-
(1) The map
 $\varphi $
is an isomorphism.
$\varphi $
is an isomorphism. -
(2) We have the following commutative diagram, where both rows are short exact sequences:

-
(3) We have
 $Z(W(k,n,m))=\langle c \rangle $
and
$Z(W(k,n,m))=\langle c \rangle $
and
 $Z(G)=\langle stu \rangle $
.
$Z(G)=\langle stu \rangle $
. -
(4) The above commutative diagram induces isomorphisms
 $$ \begin{align*}G/Z(G)\cong W(k,n,m)/ Z(W(k,n,m))=\overline{W(k,n,m)}\cong W_{k,n,m}^+.\end{align*} $$
$$ \begin{align*}G/Z(G)\cong W(k,n,m)/ Z(W(k,n,m))=\overline{W(k,n,m)}\cong W_{k,n,m}^+.\end{align*} $$
We split the proof of Theorem 3.3 into several statements.
Remark 3.4. As a byproduct, in the cases where
![]() $H=W(k,n,m)$
is finite, we recover from Theorem 3.3 the known (see for instance the tables at the end of [Reference Broué11]) description of
$H=W(k,n,m)$
is finite, we recover from Theorem 3.3 the known (see for instance the tables at the end of [Reference Broué11]) description of
![]() $H/Z(H)$
given in Table 2. Note that for the primitive groups, that is, all the groups in Table 2 except dihedral groups, there are three possible groups
$H/Z(H)$
given in Table 2. Note that for the primitive groups, that is, all the groups in Table 2 except dihedral groups, there are three possible groups
![]() $H/Z(H)$
: this is a well-known fact, as these groups are of three types, called tetrahedral (
$H/Z(H)$
: this is a well-known fact, as these groups are of three types, called tetrahedral (
![]() $G_4$
), octahedral (
$G_4$
), octahedral (
![]() $G_8, G_{12}$
), and icosahedral (
$G_8, G_{12}$
), and icosahedral (
![]() $G_{16}, G_{20}, G_{22}$
), depending on whether H is a subgroup of the tetrahedral group
$G_{16}, G_{20}, G_{22}$
), depending on whether H is a subgroup of the tetrahedral group
![]() $\mathcal {T}$
, octahedral group
$\mathcal {T}$
, octahedral group
![]() $\mathcal {O}$
, or icosahedral group
$\mathcal {O}$
, or icosahedral group
![]() $\mathcal {I}$
. If H is of type
$\mathcal {I}$
. If H is of type
![]() $\mathcal {G}$
for
$\mathcal {G}$
for
![]() $\mathcal {G}\in \{\mathcal {T}, \mathcal {O}, \mathcal {I}\}$
, then
$\mathcal {G}\in \{\mathcal {T}, \mathcal {O}, \mathcal {I}\}$
, then
![]() $H/Z(H)\cong \mathcal {G}/ Z(\mathcal {G})$
(see [Reference Lehrer and Taylor23, Ch. 6] for a detailed explanation of this phenomenon).
$H/Z(H)\cong \mathcal {G}/ Z(\mathcal {G})$
(see [Reference Lehrer and Taylor23, Ch. 6] for a detailed explanation of this phenomenon).
Table 2 Quotient of a finite toric reflection group by its center.

Remark 3.5. As another byproduct, Theorem 3.3 also gives new presentations for alternating subgroups of Coxeter groups of rank three whose Coxeter diagrams have two edges with coprime labels. That is, for
![]() $k,n,m\geq 2$
,
$k,n,m\geq 2$
,
![]() $n<m$
, and
$n<m$
, and
![]() $n,m$
are coprime, we have
$n,m$
are coprime, we have
 $$ \begin{align*} W_{k,n,m}^+=\left\langle x_1,x_2,\ldots, x_n \ \bigg\vert\ \begin{matrix} x_i^k=1 \quad \text{for all } i=1, \ldots, n,\\ x_1 x_2 \cdots x_m = x_i x_{i+1} \cdots x_{i+m-1}, \quad \text{for all } i=2, \ldots, n, \\ (x_1 x_2 \cdots x_n)^m=1. \end{matrix} \ \right\rangle \end{align*} $$
$$ \begin{align*} W_{k,n,m}^+=\left\langle x_1,x_2,\ldots, x_n \ \bigg\vert\ \begin{matrix} x_i^k=1 \quad \text{for all } i=1, \ldots, n,\\ x_1 x_2 \cdots x_m = x_i x_{i+1} \cdots x_{i+m-1}, \quad \text{for all } i=2, \ldots, n, \\ (x_1 x_2 \cdots x_n)^m=1. \end{matrix} \ \right\rangle \end{align*} $$
The following statement proves the first point of Theorem 3.3.
Proposition 3.6. The map
![]() $\varphi $
is an isomorphism.
$\varphi $
is an isomorphism.
Proof. We still denote the images of the generators
![]() $x_i$
of
$x_i$
of
![]() $W(k,n,m)$
in the quotient
$W(k,n,m)$
in the quotient
![]() $\overline {W(k,n,m)}$
by
$\overline {W(k,n,m)}$
by
![]() $x_i$
. In terms of Presentation (3-1), the map
$x_i$
. In terms of Presentation (3-1), the map
![]() $\varphi $
sends
$\varphi $
sends
![]() $x_i$
to
$x_i$
to
![]() $b^{-i+1} a b^{i-1}$
for all
$b^{-i+1} a b^{i-1}$
for all
![]() $i=1, 2, \ldots , n$
. Writing again
$i=1, 2, \ldots , n$
. Writing again
![]() $m=qn+r$
for the Euclidean division of m by n, let us observe for later use that
$m=qn+r$
for the Euclidean division of m by n, let us observe for later use that
 $$ \begin{align} \varphi(x_1 x_2\cdots x_m)&=\varphi(x_1 x_2 \cdots x_n)^q \varphi(x_1 x_2 \cdots x_r) \nonumber\\ &=(ab^{-1})^{nq}(ab^{-1})^{r-1} a b^{r-1}=(ab^{-1})^m b^r=b^r. \end{align} $$
$$ \begin{align} \varphi(x_1 x_2\cdots x_m)&=\varphi(x_1 x_2 \cdots x_n)^q \varphi(x_1 x_2 \cdots x_r) \nonumber\\ &=(ab^{-1})^{nq}(ab^{-1})^{r-1} a b^{r-1}=(ab^{-1})^m b^r=b^r. \end{align} $$
In particular, as b has order n, and r and n are coprime, the map
![]() $\varphi $
is surjective as both a and b are in the image of
$\varphi $
is surjective as both a and b are in the image of
![]() $\varphi $
.
$\varphi $
.
Let us construct the inverse
![]() $\psi $
of
$\psi $
of
![]() $\varphi $
. To this end, let
$\varphi $
. To this end, let
![]() $\ell \geq 1$
be the smallest positive integer such that
$\ell \geq 1$
be the smallest positive integer such that
![]() $(b^r)^\ell =b$
. Again, as n and r are coprime, such an integer must exist. We define
$(b^r)^\ell =b$
. Again, as n and r are coprime, such an integer must exist. We define
![]() $\psi $
on generators by
$\psi $
on generators by
![]() $a\mapsto x_1$
,
$a\mapsto x_1$
,
![]() $b\mapsto (x_1 x_2\cdots x_m)^\ell $
. Let us check that these images satisfy the defining relations of Equation (3-1). We have
$b\mapsto (x_1 x_2\cdots x_m)^\ell $
. Let us check that these images satisfy the defining relations of Equation (3-1). We have
![]() $\psi (a)^k=x_1^k=1$
and
$\psi (a)^k=x_1^k=1$
and
 $\psi (b)^n=((x_1 x_2\cdots x_m)^\ell )^n=(\underbrace {(x_1 x_2\cdots x_m)^n}_{=1})^\ell =1$
. Now we have, taking indices modulo n when necessary,
$\psi (b)^n=((x_1 x_2\cdots x_m)^\ell )^n=(\underbrace {(x_1 x_2\cdots x_m)^n}_{=1})^\ell =1$
. Now we have, taking indices modulo n when necessary,
Writing
![]() $\delta =x_1 x_2\cdots x_m$
, we have
$\delta =x_1 x_2\cdots x_m$
, we have
![]() $x_i \delta =\delta x_{i+r}$
for all
$x_i \delta =\delta x_{i+r}$
for all
![]() $i=1, \ldots , n$
by Lemma 3.2. Using this relation, one checks by induction on i, using the fact that
$i=1, \ldots , n$
by Lemma 3.2. Using this relation, one checks by induction on i, using the fact that
![]() $\ell r\equiv 1~(\mathrm {mod}~n)$
, that for
$\ell r\equiv 1~(\mathrm {mod}~n)$
, that for
![]() $i\geq 1$
, we have
$i\geq 1$
, we have
For
![]() $i=m$
, the product
$i=m$
, the product
![]() $x_{m-(m-1)m+1} x_{m-(m-1)m+2}\cdots x_{m-1} x_m$
has
$x_{m-(m-1)m+1} x_{m-(m-1)m+2}\cdots x_{m-1} x_m$
has
![]() $m(m-1)$
factors and since two consecutive factors have consecutive indices, using the defining relations
$m(m-1)$
factors and since two consecutive factors have consecutive indices, using the defining relations
![]() $x_1 x_2 \cdots x_m=x_i x_{i+1} \cdots x_{i+m-1}$
(
$x_1 x_2 \cdots x_m=x_i x_{i+1} \cdots x_{i+m-1}$
(
![]() $i\geq 2$
), we get that this product is equal to
$i\geq 2$
), we get that this product is equal to
![]() $\delta ^{m-1}$
. Hence,
$\delta ^{m-1}$
. Hence,
Now, using that
![]() $\ell r \equiv 1~(\mathrm {mod}~n)$
, we get that
$\ell r \equiv 1~(\mathrm {mod}~n)$
, we get that
![]() $m(\ell -1)+m-1\equiv 0~(\mathrm {mod}~n)$
, and hence that
$m(\ell -1)+m-1\equiv 0~(\mathrm {mod}~n)$
, and hence that
![]() $(\psi (b)\psi (a^{-1}))^m=1$
as
$(\psi (b)\psi (a^{-1}))^m=1$
as
![]() $\delta ^n=1$
. This shows that
$\delta ^n=1$
. This shows that
![]() $\psi $
is also a group homomorphism.
$\psi $
is also a group homomorphism.
It remains to show that
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
are inverse to each other. We have
$\psi $
are inverse to each other. We have
![]() $\varphi \circ \psi =\mathrm {id}$
as
$\varphi \circ \psi =\mathrm {id}$
as
![]() $a\mapsto x_1\mapsto a$
and using Equation (3-2),
$a\mapsto x_1\mapsto a$
and using Equation (3-2),
![]() $b\mapsto (x_1 x_2\cdots x_m)^\ell \mapsto (b^r)^\ell =b$
. Conversely, the map
$b\mapsto (x_1 x_2\cdots x_m)^\ell \mapsto (b^r)^\ell =b$
. Conversely, the map
![]() $\psi \circ \varphi $
maps
$\psi \circ \varphi $
maps
![]() $x_i\mapsto b^{-i+1} a b^{i-1}\mapsto \delta ^{(-i+1)\ell } x_1 \delta ^{(i-1)\ell }$
(
$x_i\mapsto b^{-i+1} a b^{i-1}\mapsto \delta ^{(-i+1)\ell } x_1 \delta ^{(i-1)\ell }$
(
![]() $i=1,\ldots , n$
). By Lemma 3.2, we have
$i=1,\ldots , n$
). By Lemma 3.2, we have
and as
![]() $\ell r\equiv 1 (\mathrm {mod}~ n)$
, we have
$\ell r\equiv 1 (\mathrm {mod}~ n)$
, we have
![]() $x_{1+(i-1)\ell r}=x_i$
, which concludes the proof.
$x_{1+(i-1)\ell r}=x_i$
, which concludes the proof.
Proof of Theorem 3.3
The isomorphism
![]() $\overline {W(k,n,m)}\cong W_{k,n,m}^+$
claimed in the first point is shown in Proposition 3.6. This also establishes that the short exact sequence in the second row of the diagram of the second point is exact—this also shows that the map
$\overline {W(k,n,m)}\cong W_{k,n,m}^+$
claimed in the first point is shown in Proposition 3.6. This also establishes that the short exact sequence in the second row of the diagram of the second point is exact—this also shows that the map
![]() $G\longrightarrow W_{k,n,m}^+$
is surjective. To show that the first row is exact, it suffices to see that the presentation
$G\longrightarrow W_{k,n,m}^+$
is surjective. To show that the first row is exact, it suffices to see that the presentation
is a presentation of
![]() $W_{k,n,m}^+$
via
$W_{k,n,m}^+$
via
![]() $s\mapsto r_1 r_2=a$
,
$s\mapsto r_1 r_2=a$
,
![]() $t\mapsto r_2 r_3=b^{-1}$
,
$t\mapsto r_2 r_3=b^{-1}$
,
![]() $u\mapsto r_3 r_1=b a^{-1}$
. However, this exactly yields Presentation (3-1). Now the commutativity of the diagram is clear: the commutativity of the square of the right is clear, and since the first row is exact, the kernel
$u\mapsto r_3 r_1=b a^{-1}$
. However, this exactly yields Presentation (3-1). Now the commutativity of the diagram is clear: the commutativity of the square of the right is clear, and since the first row is exact, the kernel
![]() $\langle c \rangle $
of
$\langle c \rangle $
of
![]() $W(k,n,m)\longrightarrow W_{k,n,m}^+$
has to be included in the kernel
$W(k,n,m)\longrightarrow W_{k,n,m}^+$
has to be included in the kernel
![]() $\langle stu \rangle $
of the first short exact sequence; this can also be seen explicitly using the fact that
$\langle stu \rangle $
of the first short exact sequence; this can also be seen explicitly using the fact that
![]() $stu$
is central in G, as
$stu$
is central in G, as
This establishes the second point. Now by Proposition 3.1, the group
![]() $W_{k,n,m}^+$
has trivial center except possibly in the cases where
$W_{k,n,m}^+$
has trivial center except possibly in the cases where
![]() $W_{k,n,m}$
is finite or not irreducible, that is, for
$W_{k,n,m}$
is finite or not irreducible, that is, for
![]() $(k,n,m)=(2,2,m)$
with m odd,
$(k,n,m)=(2,2,m)$
with m odd,
![]() $(2,3,4)$
,
$(2,3,4)$
,
![]() $(2,3,5)$
,
$(2,3,5)$
,
![]() $(3,2,3)$
,
$(3,2,3)$
,
![]() $(3,2,5)$
,
$(3,2,5)$
,
![]() $(4,2,3)$
,
$(4,2,3)$
,
![]() $(5,2,3)$
. In all cases, we get finite Coxeter groups of types
$(5,2,3)$
. In all cases, we get finite Coxeter groups of types
![]() $A_1\times I_2(m)$
(m odd),
$A_1\times I_2(m)$
(m odd),
![]() $A_3$
,
$A_3$
,
![]() $B_3$
, and
$B_3$
, and
![]() $H_3$
. The center of
$H_3$
. The center of
![]() $A_3$
is trivial, and the centers of both
$A_3$
is trivial, and the centers of both
![]() $H_3$
and
$H_3$
and
![]() $B_3$
have order two, generated by the longest element
$B_3$
have order two, generated by the longest element
![]() $w_0$
, which is not in the alternating subgroup. The center of
$w_0$
, which is not in the alternating subgroup. The center of
![]() $A_1\times I_2(m)$
is also of order two (it is the
$A_1\times I_2(m)$
is also of order two (it is the
![]() $A_1$
component) since m is odd, generated by a simple reflection; hence its nontrivial element is not in the alternating subgroup. We thus have seen that in all possible cases, the group
$A_1$
component) since m is odd, generated by a simple reflection; hence its nontrivial element is not in the alternating subgroup. We thus have seen that in all possible cases, the group
![]() $W_{k,n,m}^+$
has trivial center. This implies that the kernels of both short exact sequences are in fact the centers of the groups in the middle. This establishes point
$W_{k,n,m}^+$
has trivial center. This implies that the kernels of both short exact sequences are in fact the centers of the groups in the middle. This establishes point
![]() $3$
, and the last point is then immediate.
$3$
, and the last point is then immediate.
Remark 3.7. The idea of extending the group
![]() $G/\langle stu\rangle $
into a Coxeter group is present in work of Coxeter [Reference Coxeter14, Section 4.1].
$G/\langle stu\rangle $
into a Coxeter group is present in work of Coxeter [Reference Coxeter14, Section 4.1].
Remark 3.8. We do not know whether c has finite order in
![]() $W(k,n,m)$
or not when
$W(k,n,m)$
or not when
![]() $W(k,n,m)$
is infinite. It should be possible to establish that c has infinite order whenever
$W(k,n,m)$
is infinite. It should be possible to establish that c has infinite order whenever
![]() $W(k,n,m)$
is infinite using topological methods, by viewing
$W(k,n,m)$
is infinite using topological methods, by viewing
![]() $W(k,n,m)$
as the fundamental group of a fibered Seifert orbifold, and combining well-known results on such orbifolds. I thank Michael Heusener for pointing this out to me, explaining to me the ideas behind this approach, and providing several references on the topic. Determining whether c has finite order or not is equivalent to determining whether
$W(k,n,m)$
as the fundamental group of a fibered Seifert orbifold, and combining well-known results on such orbifolds. I thank Michael Heusener for pointing this out to me, explaining to me the ideas behind this approach, and providing several references on the topic. Determining whether c has finite order or not is equivalent to determining whether
![]() $stu$
has finite order or not in G. In Achar and Aubert’s representation (see Section 2.3), the element
$stu$
has finite order or not in G. In Achar and Aubert’s representation (see Section 2.3), the element
![]() $\rho (stu)$
has finite order since it is a scalar matrix with eigenvalue a product of three roots of unity, but we can use the observation made in Example 2.20 to see that in general, the restriction of the representation to
$\rho (stu)$
has finite order since it is a scalar matrix with eigenvalue a product of three roots of unity, but we can use the observation made in Example 2.20 to see that in general, the restriction of the representation to
![]() $\langle stu \rangle $
is unfaithful: again, consider the group
$\langle stu \rangle $
is unfaithful: again, consider the group
![]() $W(6,2,3)$
. We see that
$W(6,2,3)$
. We see that
![]() $\rho (c)=\rho ((x_1 x_2)^3)=1$
, while c cannot be equal to
$\rho (c)=\rho ((x_1 x_2)^3)=1$
, while c cannot be equal to
![]() $1$
in
$1$
in
![]() $W(6,2,3)$
.
$W(6,2,3)$
.
We end up the section with an observation on the solvability of the word problem in
![]() $W(k,n,m)$
. Recall that a group has a solvable word problem if there exists an algorithm allowing one to determine in finite time whether an arbitrary word represents the identity or not. Theorem 3.3 seems to be close to answering this question positively since
$W(k,n,m)$
. Recall that a group has a solvable word problem if there exists an algorithm allowing one to determine in finite time whether an arbitrary word represents the identity or not. Theorem 3.3 seems to be close to answering this question positively since
![]() $W(k,n,m)$
is a central extension of a subgroup of a Coxeter group (which therefore has a solvable word problem as Coxeter groups have a solvable word problem [Reference Abramenko and Brown1, Section 2.3.3]) with a cyclic group. Nevertheless, and as observed in the previous remark, the center is not clearly identified. Given any word in the generators of
$W(k,n,m)$
is a central extension of a subgroup of a Coxeter group (which therefore has a solvable word problem as Coxeter groups have a solvable word problem [Reference Abramenko and Brown1, Section 2.3.3]) with a cyclic group. Nevertheless, and as observed in the previous remark, the center is not clearly identified. Given any word in the generators of
![]() $W(k,n,m)$
, we can take its image in
$W(k,n,m)$
, we can take its image in
![]() $W_{k,n,m}^+$
and say whether it represents the identity or not, and hence solve the problem of determining whether the word we started with represents an element that lies in the center of
$W_{k,n,m}^+$
and say whether it represents the identity or not, and hence solve the problem of determining whether the word we started with represents an element that lies in the center of
![]() $W(k,n,m)$
or not. Nevertheless, if our starting word does lie in the center, it is not clear to us how to check whether it represents the identity or not.
$W(k,n,m)$
or not. Nevertheless, if our starting word does lie in the center, it is not clear to us how to check whether it represents the identity or not.
Question 3.9. Do the groups
![]() $W(k,n,m)$
have solvable word problems?
$W(k,n,m)$
have solvable word problems?
We conjecture the answer to this question to be positive.
4 Classification of toric reflection groups
The aim of this section is to show the following result.
Theorem 4.1 (Classification of toric reflection groups)
Let
![]() $k,k',n,n',m,m'\geq 2$
with
$k,k',n,n',m,m'\geq 2$
with
![]() $n<m$
,
$n<m$
,
![]() $n'<m'$
,
$n'<m'$
,
![]() $n,m$
coprime, and
$n,m$
coprime, and
![]() $n',m'$
coprime. Then
$n',m'$
coprime. Then
To this end, we require the description of the quotient of a toric reflection group by its center from the previous section, together with the following result.
Proposition 4.2 ([Reference Bourbaki8, Ch. V, Section 4, Exercise 2] or [Reference Brink and Howlett10, Proposition 1.3])
Let
![]() $(W,S)$
be a Coxeter system and
$(W,S)$
be a Coxeter system and
![]() $H\subseteq W$
a finite subgroup of W. Then there exists
$H\subseteq W$
a finite subgroup of W. Then there exists
![]() $w\in W$
and
$w\in W$
and
![]() $J\subseteq S$
such that
$J\subseteq S$
such that
![]() $W_J$
is finite and
$W_J$
is finite and
![]() $wHw^{-1}\subseteq W_J$
.
$wHw^{-1}\subseteq W_J$
.
Corollary 4.3. Let
![]() $(W,S)$
be a Coxeter system. Every increasing chain
$(W,S)$
be a Coxeter system. Every increasing chain
of finite subgroups
![]() $(H_i)_{i\geq 1}$
stabilizes, that is, there is
$(H_i)_{i\geq 1}$
stabilizes, that is, there is
![]() $n\geq 1$
such that
$n\geq 1$
such that
![]() $H_{n+p}=H_n$
for all
$H_{n+p}=H_n$
for all
![]() $p\geq 1$
.
$p\geq 1$
.
Proof. By Proposition 4.2, the cardinality of a finite subgroup of W is bounded by
which is well defined since S is finite.
Definition 4.4. Let G be a group. A subgroup
![]() $H\subseteq G$
is maximal finite if H is finite and if for every subgroup
$H\subseteq G$
is maximal finite if H is finite and if for every subgroup
![]() $H'\subseteq G$
,
$H'\subseteq G$
,
Note that maximal finite subgroups need not exist in general. By Corollary 4.3, maximal finite subgroups always exist in Coxeter groups, and we even have the stronger statement that every finite subgroup of a Coxeter group is included in a maximal finite subgroup: otherwise, one could build an increasing chain of finite subgroups that does not stabilize. Note that being a maximal finite subgroup is a property that is stable under conjugation.
Proposition 4.5. Let
![]() $(W,S)$
be a Coxeter system and
$(W,S)$
be a Coxeter system and
Then
![]() $\{ W_I~|~I\in M_W\}$
is a set of representatives of the conjugacy classes of maximal finite subgroups of W.
$\{ W_I~|~I\in M_W\}$
is a set of representatives of the conjugacy classes of maximal finite subgroups of W.
Proof. By Proposition 4.2, if
![]() $H\subseteq W$
is finite, then
$H\subseteq W$
is finite, then
![]() $w H w^{-1} \subseteq W_J$
for some
$w H w^{-1} \subseteq W_J$
for some
![]() $w\in W$
and some
$w\in W$
and some
![]() $J\subseteq S$
such that
$J\subseteq S$
such that
![]() $W_J$
is finite. To conclude the proof, it therefore suffices to show that for
$W_J$
is finite. To conclude the proof, it therefore suffices to show that for
![]() $I\in M_W$
, the subgroup
$I\in M_W$
, the subgroup
![]() $W_I$
is maximal finite, and that for
$W_I$
is maximal finite, and that for
![]() $I\neq J$
where
$I\neq J$
where
![]() $I,J\in M_W$
, the subgroups
$I,J\in M_W$
, the subgroups
![]() $W_I$
and
$W_I$
and
![]() $W_J$
are not conjugate to each other. This last property is a consequence of [Reference Krammer22, Corollary 3.1.7], as I is a maximal subset of S such that
$W_J$
are not conjugate to each other. This last property is a consequence of [Reference Krammer22, Corollary 3.1.7], as I is a maximal subset of S such that
![]() $W_I$
is finite. Now let us show that
$W_I$
is finite. Now let us show that
![]() $W_I$
,
$W_I$
,
![]() $I\in M_W$
, is maximal finite. Let
$I\in M_W$
, is maximal finite. Let
![]() $W_I\subseteq H$
such that H is a finite subgroup of W. By Proposition 4.2, there is
$W_I\subseteq H$
such that H is a finite subgroup of W. By Proposition 4.2, there is
![]() $J\subseteq S$
and
$J\subseteq S$
and
![]() $w\in W$
such that
$w\in W$
such that
![]() $W_J$
is finite and
$W_J$
is finite and
![]() $W_I\subseteq H \subseteq w^{-1} W_J w$
. Writing
$W_I\subseteq H \subseteq w^{-1} W_J w$
. Writing
![]() $w_1$
for the unique element of minimal length in
$w_1$
for the unique element of minimal length in
![]() $W_J w W_I$
, we have
$W_J w W_I$
, we have
![]() $I\cap w_1^{-1} J w_1=I$
by [Reference Abramenko and Brown1, Lemma 2.25], and hence
$I\cap w_1^{-1} J w_1=I$
by [Reference Abramenko and Brown1, Lemma 2.25], and hence
![]() $I\subseteq w_1^{-1} J w_1$
. Let
$I\subseteq w_1^{-1} J w_1$
. Let
![]() ${I'\subseteq J}$
such that
${I'\subseteq J}$
such that
![]() $I=w_1 I' w_1^{-1}$
. Then since
$I=w_1 I' w_1^{-1}$
. Then since
![]() $W_I$
and
$W_I$
and
![]() $W_{I'}$
cannot be conjugate to each other if
$W_{I'}$
cannot be conjugate to each other if
![]() $I\neq I'$
because of the maximality of I (again by [Reference Krammer22, Corollary 3.1.7]), we have
$I\neq I'$
because of the maximality of I (again by [Reference Krammer22, Corollary 3.1.7]), we have
![]() $I'=I$
, and hence
$I'=I$
, and hence
![]() $I\subseteq J$
, which forces
$I\subseteq J$
, which forces
![]() $I=J$
since
$I=J$
since
![]() $W_J$
is finite. Since
$W_J$
is finite. Since
![]() $W_I$
and
$W_I$
and
![]() $w^{-1} W_J w=w^{-1} W_I w$
have the same cardinality and
$w^{-1} W_J w=w^{-1} W_I w$
have the same cardinality and
![]() $W_I\subseteq H\subseteq w^{-1} W_J w$
, we get
$W_I\subseteq H\subseteq w^{-1} W_J w$
, we get
![]() $H=W_I$
.
$H=W_I$
.
Note that since every increasing chain of finite subgroups of a Coxeter group W stabilizes, the same is true for any subgroup of W; in particular it holds true for
![]() $W^+$
. Specifically, there are maximal finite subgroups in
$W^+$
. Specifically, there are maximal finite subgroups in
![]() $W^+$
, and every finite subgroup of
$W^+$
, and every finite subgroup of
![]() $W^+$
is included in a maximal finite one.
$W^+$
is included in a maximal finite one.
Proposition 4.6. Let
![]() $k,n,m\geq 2$
be such that
$k,n,m\geq 2$
be such that
![]() $W_{k,n,m}$
is infinite. There are three conjugacy classes of maximal finite subgroups of
$W_{k,n,m}$
is infinite. There are three conjugacy classes of maximal finite subgroups of
![]() $W_{k,n,m}^+$
. The finite groups in these three classes are isomorphic to
$W_{k,n,m}^+$
. The finite groups in these three classes are isomorphic to
![]() $C_k$
,
$C_k$
,
![]() $C_n$
,
$C_n$
,
![]() $C_m$
, where
$C_m$
, where
![]() $C_i$
denotes the cyclic group of order i.
$C_i$
denotes the cyclic group of order i.
Proof. Note that under these assumptions, the Coxeter group
![]() $W=W_{k,n,m}$
is irreducible. Moreover, in this case,
$W=W_{k,n,m}$
is irreducible. Moreover, in this case,
![]() $M_W$
consists of the three subsets of S of cardinality two as
$M_W$
consists of the three subsets of S of cardinality two as
![]() $|S|=3$
and W is infinite. Let
$|S|=3$
and W is infinite. Let
![]() $H\subseteq W_{k,n,m}^+$
be a finite subgroup of
$H\subseteq W_{k,n,m}^+$
be a finite subgroup of
![]() $W_{k,n,m}^+$
. We claim that H is a conjugate (in
$W_{k,n,m}^+$
. We claim that H is a conjugate (in
![]() $W_{k,n,m}^+$
) of a subgroup of the alternating subgroup
$W_{k,n,m}^+$
) of a subgroup of the alternating subgroup
![]() $W_J^+$
of a standard parabolic subgroup
$W_J^+$
of a standard parabolic subgroup
![]() $W_J$
of rank two of
$W_J$
of rank two of
![]() $W_{k,n,m}$
. If
$W_{k,n,m}$
. If
![]() $H=1$
, the claim is trivially true; hence assume that
$H=1$
, the claim is trivially true; hence assume that
![]() $H\neq 1$
. By Proposition 4.2, there is
$H\neq 1$
. By Proposition 4.2, there is
![]() $w\in W_{k,n,m}$
such that
$w\in W_{k,n,m}$
such that
![]() $wHw^{-1}\subseteq W_J$
for some
$wHw^{-1}\subseteq W_J$
for some
![]() $J\subseteq S$
such that
$J\subseteq S$
such that
![]() $W_J$
is finite. If
$W_J$
is finite. If
![]() $w\in W_{k,n,m}^+$
, then H and
$w\in W_{k,n,m}^+$
, then H and
![]() $wHw^{-1}$
are conjugate in
$wHw^{-1}$
are conjugate in
![]() $W_{k,n,m}^+$
, and hence the claim holds true. If
$W_{k,n,m}^+$
, and hence the claim holds true. If
![]() $w\notin W_{k,n,m}^+$
, then since
$w\notin W_{k,n,m}^+$
, then since
![]() $H\neq 1$
, we have
$H\neq 1$
, we have
![]() $J\neq \emptyset $
, so let
$J\neq \emptyset $
, so let
![]() $s\in J$
. Then
$s\in J$
. Then
![]() $sw\in W_{k,n,m}^+$
and
$sw\in W_{k,n,m}^+$
and
![]() $sw H w^{-1}s\subseteq s W_J s= W_J$
, and hence H is again conjugate in
$sw H w^{-1}s\subseteq s W_J s= W_J$
, and hence H is again conjugate in
![]() $W_{k,n,m}^+$
to a subgroup of
$W_{k,n,m}^+$
to a subgroup of
![]() $W_J$
. In all cases, since
$W_J$
. In all cases, since
![]() $1\neq H\subseteq W_{k,n,m}^+$
and
$1\neq H\subseteq W_{k,n,m}^+$
and
![]() $W_J$
is finite, we must have
$W_J$
is finite, we must have
![]() $|J|=2$
since for
$|J|=2$
since for
![]() $|J|=1$
, we have
$|J|=1$
, we have
![]() $W_J\cap W_{k,n,m}^+=\{1\}$
. Therefore, H is conjugate to a subgroup of the alternating subgroup of one of the three standard parabolic subgroups of rank
$W_J\cap W_{k,n,m}^+=\{1\}$
. Therefore, H is conjugate to a subgroup of the alternating subgroup of one of the three standard parabolic subgroups of rank
![]() $2$
of
$2$
of
![]() $W_{k,n,m}$
. Note that these parabolic subgroups are dihedral groups of orders
$W_{k,n,m}$
. Note that these parabolic subgroups are dihedral groups of orders
![]() $2k, 2n$
, and
$2k, 2n$
, and
![]() $2m$
. It follows that there are at most three conjugacy classes of maximal finite subgroups of
$2m$
. It follows that there are at most three conjugacy classes of maximal finite subgroups of
![]() $W_{k,n,m}^+$
, since if H is maximal finite, then it has to be a conjugate of one of these alternating subgroups, namely
$W_{k,n,m}^+$
, since if H is maximal finite, then it has to be a conjugate of one of these alternating subgroups, namely
![]() $C_k$
,
$C_k$
,
![]() $C_n$
, or
$C_n$
, or
![]() $C_m$
.
$C_m$
.
To conclude the proof, it therefore remains to show that the above three alternating subgroups of standard parabolic subgroups of rank two of
![]() $W_{k,n,m}$
are maximal finite subgroups of
$W_{k,n,m}$
are maximal finite subgroups of
![]() $W_{k,n,m}^+$
that are not conjugate to each other—in fact, we show that they are not conjugate in
$W_{k,n,m}^+$
that are not conjugate to each other—in fact, we show that they are not conjugate in
![]() $W_{k,n,m}$
, which is stronger. Maximality follows again from Proposition 4.2: let
$W_{k,n,m}$
, which is stronger. Maximality follows again from Proposition 4.2: let
![]() $J\subseteq S$
with
$J\subseteq S$
with
![]() $|J|=2$
. Then if
$|J|=2$
. Then if
![]() $W_J^{+}\subseteq W_J$
is not maximal finite inside
$W_J^{+}\subseteq W_J$
is not maximal finite inside
![]() $W_{k,n,m}^+$
, then there is a finite subgroup H of
$W_{k,n,m}^+$
, then there is a finite subgroup H of
![]() $W_{k,n,m}^+$
such that
$W_{k,n,m}^+$
such that
![]() $W_J^+\subsetneq H$
. By Proposition 4.2, the subgroup H is included in a finite parabolic subgroup
$W_J^+\subsetneq H$
. By Proposition 4.2, the subgroup H is included in a finite parabolic subgroup
![]() $x W_{J'} x^{-1}$
and up to enlarging
$x W_{J'} x^{-1}$
and up to enlarging
![]() $J'$
, we can assume that
$J'$
, we can assume that
![]() $|J'|=2$
(alternatively we can use the fact that every finite subgroup of
$|J'|=2$
(alternatively we can use the fact that every finite subgroup of
![]() $W_{k,n,m}$
is included in a maximal finite one together with Proposition 4.5). Writing
$W_{k,n,m}$
is included in a maximal finite one together with Proposition 4.5). Writing
![]() $J=\{t_1, t_2\}$
, we have
$J=\{t_1, t_2\}$
, we have
![]() $t_1 t_2\in W_J^{+}\subseteq H\subseteq x W_{J'} x^{-1}$
. Now the intersection of two parabolic subgroups is again a parabolic subgroup (see for instance [Reference Abramenko and Brown1, Lemma 2.25]), and hence we have that
$t_1 t_2\in W_J^{+}\subseteq H\subseteq x W_{J'} x^{-1}$
. Now the intersection of two parabolic subgroups is again a parabolic subgroup (see for instance [Reference Abramenko and Brown1, Lemma 2.25]), and hence we have that
![]() $W_J\cap x W_{J'} x^{-1}$
is finite parabolic of rank at most two. However, since it contains
$W_J\cap x W_{J'} x^{-1}$
is finite parabolic of rank at most two. However, since it contains
![]() $t_1 t_2$
, it must have rank
$t_1 t_2$
, it must have rank
![]() $2$
. As rank two parabolic subgroups are maximal finite by Proposition 4.5, we have that both
$2$
. As rank two parabolic subgroups are maximal finite by Proposition 4.5, we have that both
![]() $W_J$
,
$W_J$
,
![]() $x W_{J'} x^{-1}$
and
$x W_{J'} x^{-1}$
and
![]() $W_J\cap x W_{J'} x^{-1}$
are maximal finite, which forces
$W_J\cap x W_{J'} x^{-1}$
are maximal finite, which forces
![]() $W_J=x W_{J'} x^{-1}$
. Hence,
$W_J=x W_{J'} x^{-1}$
. Hence,
![]() $W_J^{+}\subseteq H \subseteq W_J$
, which forces
$W_J^{+}\subseteq H \subseteq W_J$
, which forces
![]() $H=W_J^+$
as
$H=W_J^+$
as
![]() $H\subseteq W_{k,n,m}^+$
. Therefore,
$H\subseteq W_{k,n,m}^+$
. Therefore,
![]() $W_J^+$
is maximal finite. Now for
$W_J^+$
is maximal finite. Now for
![]() $J_1\neq J_2$
with
$J_1\neq J_2$
with
![]() $J_i\subseteq S$
and
$J_i\subseteq S$
and
![]() $|J_1|=2=|J_2|$
, we see that
$|J_1|=2=|J_2|$
, we see that
![]() $W_{J_1}^+$
and
$W_{J_1}^+$
and
![]() $W_{J_2}^+$
cannot be conjugate to each other in W: if this was the case, there would be
$W_{J_2}^+$
cannot be conjugate to each other in W: if this was the case, there would be
![]() $x\in W$
such that
$x\in W$
such that
![]() $W_{J_1}^+ \subseteq x W_{J_2} x^{-1}$
, and arguing as above (with
$W_{J_1}^+ \subseteq x W_{J_2} x^{-1}$
, and arguing as above (with
![]() $J=J_1$
and
$J=J_1$
and
![]() $J'=J_2$
), we would get that
$J'=J_2$
), we would get that
![]() $W_{J_1}$
and
$W_{J_1}$
and
![]() $W_{J_2}$
are conjugate to each other, contradicting Proposition 4.5.
$W_{J_2}$
are conjugate to each other, contradicting Proposition 4.5.
Proof of Theorem 4.1
Assume
![]() $W(k,n,m)\cong _{\mathrm {ref}} W(k',n',m')$
. We first claim that
$W(k,n,m)\cong _{\mathrm {ref}} W(k',n',m')$
. We first claim that
![]() $k-1$
is the number of conjugacy classes of reflections in
$k-1$
is the number of conjugacy classes of reflections in
![]() $W(k,n,m)$
. Indeed, all generators
$W(k,n,m)$
. Indeed, all generators
![]() $x_i$
are conjugate to each other, and by Theorem 2.12, we have that
$x_i$
are conjugate to each other, and by Theorem 2.12, we have that
![]() $x_1$
is the generator s of the isomorphic J-group
$x_1$
is the generator s of the isomorphic J-group
![]() $H=J(\begin {smallmatrix} k & n & m\\ ~& n& m\end {smallmatrix})\trianglelefteq J(\begin {smallmatrix} k & n & m\\ ~& ~& ~\end {smallmatrix})=G$
. We have that s has order k in G. To conclude, since reflections in
$H=J(\begin {smallmatrix} k & n & m\\ ~& n& m\end {smallmatrix})\trianglelefteq J(\begin {smallmatrix} k & n & m\\ ~& ~& ~\end {smallmatrix})=G$
. We have that s has order k in G. To conclude, since reflections in
![]() $W(k,n,m)$
are defined to be the conjugates of the nontrivial powers of the elements
$W(k,n,m)$
are defined to be the conjugates of the nontrivial powers of the elements
![]() $x_i$
, it therefore suffices to show that no two reflections in
$x_i$
, it therefore suffices to show that no two reflections in
![]() $\{s, s^2, \ldots , s^{k-1}\}$
are conjugate to each other. This holds true in G by Lemma 2.5, and hence it holds true a fortiori in H. Since reflection isomorphisms map reflections to reflections, we deduce that
$\{s, s^2, \ldots , s^{k-1}\}$
are conjugate to each other. This holds true in G by Lemma 2.5, and hence it holds true a fortiori in H. Since reflection isomorphisms map reflections to reflections, we deduce that
![]() $k=k'$
.
$k=k'$
.
Now, by Theorem 3.3, the group
![]() $\overline {W}(k,n,m)$
is the quotient of
$\overline {W}(k,n,m)$
is the quotient of
![]() $W(k,n,m)$
by its center. We therefore have
$W(k,n,m)$
by its center. We therefore have
In particular, we have
![]() $W_{k,n,m}^+\cong W_{k,n',m'}^+$
. We conclude by showing that this forces
$W_{k,n,m}^+\cong W_{k,n',m'}^+$
. We conclude by showing that this forces
![]() $n=n'$
and
$n=n'$
and
![]() $m=m'$
. We first assume that
$m=m'$
. We first assume that
![]() $W_{k,n,m}$
is infinite, which forces
$W_{k,n,m}$
is infinite, which forces
![]() $W_{k,n',m'}$
to be also infinite since alternating subgroups of Coxeter groups are subgroups of index two. By Proposition 4.6, there are three conjugacy classes of maximal finite subgroups of
$W_{k,n',m'}$
to be also infinite since alternating subgroups of Coxeter groups are subgroups of index two. By Proposition 4.6, there are three conjugacy classes of maximal finite subgroups of
![]() $W_{k,n,m}^+$
(respectively
$W_{k,n,m}^+$
(respectively
![]() $W_{k,n',m'}^+$
), and the isomorphism type of these finite subgroups is given by
$W_{k,n',m'}^+$
), and the isomorphism type of these finite subgroups is given by
![]() $C_k, C_n$
, and
$C_k, C_n$
, and
![]() $C_m$
(respectively
$C_m$
(respectively
![]() $C_k, C_{n'}$
, and
$C_k, C_{n'}$
, and
![]() $C_{m'}$
). The multiset of isomorphism type of subgroups in conjugacy classes of maximal finite subgroups is obviously invariant under isomorphism, which implies that the multisets
$C_{m'}$
). The multiset of isomorphism type of subgroups in conjugacy classes of maximal finite subgroups is obviously invariant under isomorphism, which implies that the multisets
![]() $\{k,n,m\}$
and
$\{k,n,m\}$
and
![]() $\{k,n',m'\}$
are equal. Since
$\{k,n',m'\}$
are equal. Since
![]() $n<m$
and
$n<m$
and
![]() $n'<m'$
, this forces
$n'<m'$
, this forces
![]() $n=n'$
and
$n=n'$
and
![]() $m=m'$
.
$m=m'$
.
We now assume that
![]() $W_{k,n,m}$
(and hence
$W_{k,n,m}$
(and hence
![]() $W_{k,n',m'}$
) is finite. We then deduce from Table 2 that no two groups
$W_{k,n',m'}$
) is finite. We then deduce from Table 2 that no two groups
![]() $W_{k,n,m}^+$
and
$W_{k,n,m}^+$
and
![]() $W_{k,n',m'}^+$
are isomorphic when
$W_{k,n',m'}^+$
are isomorphic when
![]() $(n',m')\neq (n,m)$
. Hence,
$(n',m')\neq (n,m)$
. Hence,
![]() $n=n'$
and
$n=n'$
and
![]() $m=m'$
.
$m=m'$
.
Remark 4.7. Mimicking the definition given for finite complex reflection groups in [Reference Broué, Malle and Rouquier12], one can define a Hecke algebra
![]() $\mathcal {H}_{k,n,m}$
of a toric reflection group
$\mathcal {H}_{k,n,m}$
of a toric reflection group
![]() $W(k,n,m)$
over a suitable base ring, deforming the group algebra
$W(k,n,m)$
over a suitable base ring, deforming the group algebra
![]() $\mathbb {Z}[W(k,n,m)]$
. It is tempting to conjecture that this algebra is a free module over this ring, with a basis deforming the basis of
$\mathbb {Z}[W(k,n,m)]$
. It is tempting to conjecture that this algebra is a free module over this ring, with a basis deforming the basis of
![]() $\mathbb {Z}[W(k,n,m)]$
given by the elements of the group
$\mathbb {Z}[W(k,n,m)]$
given by the elements of the group
![]() $W(k,n,m)$
. However, already in the finite case, the proof of the BMR freeness conjecture for those finite complex reflection groups that are toric reflection groups is case-by-case.
$W(k,n,m)$
. However, already in the finite case, the proof of the BMR freeness conjecture for those finite complex reflection groups that are toric reflection groups is case-by-case.
Remark 4.8. The parameter
![]() $k-1$
is the number of conjugacy classes of reflections in
$k-1$
is the number of conjugacy classes of reflections in
![]() $W(k,n,m)$
. It would be desirable to have an interpretation of n and m in terms of the ‘reflection group’ structure of
$W(k,n,m)$
. It would be desirable to have an interpretation of n and m in terms of the ‘reflection group’ structure of
![]() $W(k,n,m)$
. When
$W(k,n,m)$
. When
![]() $W(k,n,m)$
is finite, the parameter n is the reflection rank of
$W(k,n,m)$
is finite, the parameter n is the reflection rank of
![]() $W(k,n,m)$
, that is, the minimal number of reflections that are needed to generate
$W(k,n,m)$
, that is, the minimal number of reflections that are needed to generate
![]() $W(k,n,m)$
. We can conjecture that this still holds true for arbitrary toric reflection groups. This would be a first step toward a proof of Theorem 4.1 avoiding a recourse to the theory of Coxeter groups—which has other advantages, as for instance rank three Coxeter groups have nice geometric realizations. It would also reprove that the meridional rank of the torus knot
$W(k,n,m)$
. We can conjecture that this still holds true for arbitrary toric reflection groups. This would be a first step toward a proof of Theorem 4.1 avoiding a recourse to the theory of Coxeter groups—which has other advantages, as for instance rank three Coxeter groups have nice geometric realizations. It would also reprove that the meridional rank of the torus knot
![]() $T_{n,m}$
(
$T_{n,m}$
(
![]() $n<m$
) is equal to n (this fact is proven in [Reference Rost and Zieschang30] in the context of the meridional rank conjecture): it is indeed at most n since
$n<m$
) is equal to n (this fact is proven in [Reference Rost and Zieschang30] in the context of the meridional rank conjecture): it is indeed at most n since
![]() $G(n,m)$
has its classical presentation having exactly n meridians as generators, and if it was smaller, then because of the surjection
$G(n,m)$
has its classical presentation having exactly n meridians as generators, and if it was smaller, then because of the surjection
![]() $G(n,m)\twoheadrightarrow W(k,n,m)$
which maps meridians to reflections, the groups
$G(n,m)\twoheadrightarrow W(k,n,m)$
which maps meridians to reflections, the groups
![]() $W(k,n,m)$
could then be generated by less than n reflections. As other J-groups might be reflection quotients of other link groups, this could be of interest, even if in the specific case of torus knot groups everything seems to be already known.
$W(k,n,m)$
could then be generated by less than n reflections. As other J-groups might be reflection quotients of other link groups, this could be of interest, even if in the specific case of torus knot groups everything seems to be already known.
Acknowledgments
I thank Anne-Marie Aubert for an email exchange on J-groups. I thank Jean Michel for bringing reference [Reference Malle and Michel25] to my attention. I thank Gunter Malle for his careful reading of the manuscript and suggestions. The unfaithfulness of Achar and Aubert’s representation, discussed in Section 2.3, was easy to establish after noticing that Coxeter’s representation from [Reference Coxeter15] is unfaithful: this last property was noticed during discussions with Vincent Beck on truncated braid groups. I also thank him. I also thank Igor Haladjian for his careful reading of the manuscript and for pointing out an error in a previous version of Proposition 2.9. I thank Michael Heusener for suggesting to look at toric reflection groups as fundamental groups of fibered Seifert orbifolds. Finally, I thank the reviewer for their careful reading and insightful suggestions.