Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-23T13:26:57.374Z Has data issue: false hasContentIssue false
  • English
  • Français

TOPOLOGY OF THE REPRESENTATION VARIETIES WITH BOREL MOLD FOR UNSTABLE CASES

Part of: Families, fibrations Representation theory of groups

Published online by Cambridge University Press:  11 October 2011

KAZUNORI NAKAMOTO  and
TAKESHI TORII
KAZUNORI NAKAMOTO*
Affiliation:
Center for Life Science Research, University of Yamanashi, Yamanashi 409-3898, Japan (email: [email protected])
TAKESHI TORII
Affiliation:
Department of Mathematics, Okayama University, Okayama 700-8530, Japan (email: [email protected])
*
✉For correspondence; e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we show that, in the stable case, when m≥2n−1, the cohomology ring H*(Repn(m)B) of the representation variety with Borel mold Repn(m)B and 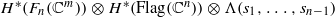are isomorphic as algebras. Here the degree of si is 2m−3 when 1≤i<n. In the unstable cases, when m≤2n−2, we also calculate the cohomology group H*(Repn(m)B) when n=3,4 . In the most exotic case, when m=2 , Rep n (2)B is homotopy equivalent to Fn (ℂ2)×PGL n (ℂ) , where Fn (ℂ2)is the configuration space of n distinct points in ℂ2. We regard Rep n (2)B as a scheme over ℤ, and show that the Picard group Pic (Rep n (2)B)of Rep n (2)B is isomorphic to ℤ/nℤ. We give an explicit generator of the Picard group.

Keywords

moduli of representationsrepresentation varietyBorel moldfree monoid

MSC classification

Secondary: 14D22: Fine and coarse moduli spaces 20C99: None of the above, but in this section
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 91 , Issue 1 , August 2011 , pp. 55 - 87
Copyright
Copyright © Australian Mathematical Publishing Association Inc. 2011

References

[1]Fricke, R. and Klein, F., Vorlesungen über die Theorie der Automorphen Funktionen, Vol. 1 (B. G. Teubner, Leipzig, 1897).Google Scholar
[2]Fröhlich, A. and Taylor, M. J., Algebraic Number Theory, Cambridge Studies in Advanced Mathematics, 27 (Cambridge University Press, Cambridge, 1993).Google Scholar
[3]Hartshorne, R., Algebraic Geometry, Graduate Texts in Mathematics, 52 (Springer, New York–Heidelberg, 1977).CrossRefGoogle Scholar
[4]Hirzebruch, F., Topological Methods in Algebraic Geometry (Springer, New York, 1966).Google Scholar
[5]King, A. D., ‘Moduli of representations of finite dimensional algebras’, Q. J. Math. Oxf. II Ser. 45 (1994), 515–530.CrossRefGoogle Scholar
[6]Nakamoto, K., ‘The moduli of representations with Borel mold’, arXiv:1008.0242.Google Scholar
[7]Nakamoto, K., ‘Representation varieties and character varieties’, Publ. Res. Inst. Math. Sci. 36 (2000), 159–189.CrossRefGoogle Scholar
[8]Nakamoto, K. and Torii, T., ‘Rational homotopy type of the moduli of representations with Borel mold’, Forum Math., in press; doi:10.1515/FORM.2011.071.CrossRefGoogle Scholar
[9]Nakamoto, K. and Torii, T., ‘Topology of the moduli of representations with Borel mold’, Pacific J. Math. 213 (2004), 365–387.CrossRefGoogle Scholar
[10]Narasimhan, M. S. and Seshadri, C. S., ‘Holomorphic vector bundles on a compact Riemann surface’, Math. Ann. 155 (1964), 69–80.CrossRefGoogle Scholar
[11]Narasimhan, M. S. and Seshadri, C. S., ‘Stable and unitary vector bundles on a compact Riemann surface’, Ann. of Math. (2) 82 (1965), 540–567.CrossRefGoogle Scholar
[12]Takagi, T., ‘Shotô Seisûron Kougi’, in: Lecture on Elementary Number Theory, 2nd edn (Kyoritsu Shuppan, Tokyo, 1971), in Japanese.Google Scholar