Hostname: page-component-f554764f5-rj9fg Total loading time: 0 Render date: 2025-04-08T23:05:28.973Z Has data issue: false hasContentIssue false
  • English
  • Français

Toeplitz Determinants and Szegö's Formula

Published online by Cambridge University Press:  09 April 2009

R. E. Hartwig
R. E. Hartwig
Affiliation:
The University of AdelaideAdelaide
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper the Toeplitz determinant of order s ≧ 1 generated by the rational function , with , and , is evaluated exactly for all values of s ≧ m, as 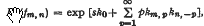, where in with and , thus proving Szegö's formula for the function fm, n(z).

By forming the rational approximation of the generating function the formula is then extended to enabling the evaluation of the limit of Toeplitz determinants generated by certain classes of complex valued functions.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 9 , Issue 1-2 , February 1969 , pp. 62 - 99
Copyright
Copyright © Australian Mathematical Society 1969

References

[1]Toeplitz, O., ‘Theorie der L-Formen’, Math. Ann. 70 (1910), 351–376.CrossRefGoogle Scholar
[2]Grenander, U. and Szegö, G., ‘Toeplitz forms and their applications’ (University of California Press, and Cambridge University Press, Cambridge, England, 1950).Google Scholar
[3]Szegö, G., ‘On certain Hermitian forms associated with the Fourier series of a positive function’, Communications du séminaire mathématique de l'université de Lund, tome supplémentaire (1952), 228–238.Google Scholar
[4]van der Waerden, B. L., ‘Modern algebra’, (Frederick Ungar Publishing Co., New York, 1948), vol. 1, p. 83).Google Scholar
[5]Green, H. S., ‘The long-range correlations of various Ising lattices’, Z. Phys. 171 (1963), 129–148.CrossRefGoogle Scholar
[6]Kaufman, B. and Onsager, L., ‘Long-range order’ (unpublished).Google Scholar
[7]Kadanoff, L. P., ‘Spin-Spin Correlation in the Two Dimensional Ising Model’, Il Nuovo Cimento 44 (1966), 276–305.CrossRefGoogle Scholar
[8]Gibberd, R. W. and Hurst, C. A., ‘A new approach to the Ising model’, J. Math. Phys. 8 (1967), 1427–1435.CrossRefGoogle Scholar
[9]Gantmacher, F. R., Theory of matrices (Chelsea, New York, 1959, vol. 2, Sec. 7, p. 196) (see also revised edition).Google Scholar
[10]Muir, T. and Metzler, W. H., Treatise on the theory of determinants (Albany, New York, 1930 (privately published), Secs. 81 and 465).Google Scholar
[11]Titchmarsh, E. C., The theory of functions, (Oxford, 1939), second edition, Sec. 3.45, p. 119).Google Scholar
[12]Szegö, G., ‘Ein Grenzwertsatz über die Toeplitzschen Determinanten einer reellen positiven Funktion’, Math. Ann. 76 (1915), 490–503.Google Scholar
[13]de la Vallée Poussin, C., Leçons sur l'Approximation des functions d'une variable réelle (Gauthier-Villards, Paris, 1919, Secs. 12, 21).Google Scholar
[14]Montroll, E. W., Potts, R. B. and Ward, J. C., ‘Correlations and Spontaneous Magnetization of the Two-Dimensional Ising Model’, J. of Math. Phus. 4 (1963), 308–322.CrossRefGoogle Scholar
[15]Kac, M., ‘Toeplitz matrices, translation kernels, and a related problem in probaility theory’, Duke Math. J., 21 (1954), 501–509.Google Scholar
[16]Kac, M., Probability and Related Topics in Physical Sciences (Interscience Publishers, New York, 1959), 40–57.Google Scholar
[17]Baxter, G., ‘Polynomials defined by a difference system’, J. Math. Anal. and Appl., 2 (1961), 223–263.CrossRefGoogle Scholar
[18]Baxter, G., ‘A convergence equivalence related to polynomials orthogonal on the unit circle’, Trans. Amer. Math. Soc., 99 (1961), 471–487.Google Scholar
[19]Baxter, G., ‘A norm inequality for a ‘finite section’ Wiener-Hopf equation’, Illinois J. of Math., 7 (1963), 97–103.CrossRefGoogle Scholar
[20]Hirschman, I. I. Jr, ‘The strong Szegö limit theorem for Toeplitz determinants’, Amer. J. Math., 88 (1966), 577–614.Google Scholar
[21]Devinatz, A., ‘The strong Szegö limit theorem’, Illinois J. of Math., 11 (1967), 160–175.CrossRefGoogle Scholar
[22]Hirschman, I. I. Jr, ‘Recent developments in the theory of finite Toeplitz operators’, to be published.Google Scholar
[23]Ryazanov, G. V., ‘Correlation asymptotics for a plane Ising lattice’, Sov. Phys. JETP, 22 (1966), 789–795.Google Scholar
[24]Wu, T. T., ‘Theory of Toeplitz determinants and spin correlations of the two-dimensional Ising model I’, Phys. Rev., 149 (1966), 380–401.CrossRefGoogle Scholar
[25]McCoy, B. M. and Wu, T. T., ‘Theory of Toeplitz determinants and spin correlations of the two-dimensional Ising model II’, Phys. Rev. 155 (1967), 438–452.CrossRefGoogle Scholar
[26]Cheng, H. and Wu, T. T., ‘Theory of Toeplitz determinants and spin correlations of the two-dimensional Ising model III’, Phys. Rev., 164 (1967), 719–735.CrossRefGoogle Scholar
[27]McCoy, B. M. and Wu, T. T., ‘Theory of Toeplitz determinants and spin correlations of the two-dimensional Ising model IV’, Phys. Rev., 162 (1967), 436–475.CrossRefGoogle Scholar