Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-06T07:13:14.231Z Has data issue: false hasContentIssue false
  • English
  • Français

Three proofs of Minkowski's second inequality in the geometry of numbers

Published online by Cambridge University Press:  09 April 2009

R. P. Bambah ,
Alan Woods  and
Hans Zassenhaus
R. P. Bambah
Affiliation:
The Ohio State University, Columbus, Ohio
Alan Woods
Affiliation:
The Ohio State University, Columbus, Ohio
Hans Zassenhaus
Affiliation:
The Ohio State University, Columbus, Ohio
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let K be a bounded, open convex set in euclidean n-space Rn, symmetric in the origin 0. Further let L be a lattice in Rn containing 0 and put extended over all positive real numbers ui for which uiK contains i linearly independent points of L. Denote the Jordan content of K by V(K) and the determinant of L by d(L). Minkowski's second inequality in the geometry of numbers states that 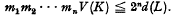Minkowski's original proof has been simplified by Weyl [6] and Cassels [7] and a different proof hasbeen given by Davenport [1].

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 5 , Issue 4 , November 1965 , pp. 453 - 462
Copyright
Copyright © Australian Mathematical Society 1965

References

[1]Davenport, H., Minkowski's inequality for the minimum associated with a convex body, Quart. J. Math. Oxford 10 (1939), 119–121.Google Scholar
[2]Mahler, K., Über die Annäherung algebraischer Zahlen durch periodische Algorithmen, Acta Mathematica 68 (1937), 109–144.CrossRefGoogle Scholar
[3]Minkowski, H., Geometrie der Zahlen, Teubner 1896, Chapter 5.Google Scholar
[4]Siegel, C. L., Geometry of Numbers, Lectures at New York University.Google Scholar
[5]Zassenhaus, H., Modern developments in the Geometry of Numbers, Bull. Am. Math. Soc. 67 (1961), 427–439.CrossRefGoogle Scholar
[6]Weyl, H., On geometry of numbers, Proc. Lond. Math. Soc. (2) 47 (1939–1940), 268–289.Google Scholar
[7]Cassels, J. W. S., An Introduction to the geometry of numbers, Springer, 1959.CrossRefGoogle Scholar