No CrossRef data available.
Article contents
Three bimodules for Mansfield's imprimitivity theorem
Part of:
Selfadjoint operator algebras
Published online by Cambridge University Press: 09 April 2009
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
For a maximal coaction δ of a discrete group G on a C*-algebra A and a normal subgroup N of G, there are at least three natural A × G ×δ| N - A ×δ|1 G/N imprimitivity bimodules: Mansfield's bimodule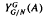 
; the bimodule assembled by Ng from Green's 
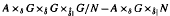imprimitivity bimodule 
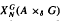and Katayama duality; and the bimodule assembled from 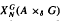and the crossed-product Mansfield bimodule 
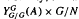. We show that all three of these are isomorphic, so that the corresponding inducing maps on representations are identical. This can be interpreted as saying that Mansfield and Green induction are inverses of one another ‘modulo Katayama duality’. These results pass to twisted coactions; dual results starting with an action are also given.
Keywords
MSC classification
Secondary:
46L55: Noncommutative dynamical systems
- Type
- Research Article
- Information
- Journal of the Australian Mathematical Society , Volume 71 , Issue 3 , December 2001 , pp. 397 - 420
- Copyright
- Copyright © Australian Mathematical Society 2001
References
[1]Echterhoff, S., Kaliszewski, S. and Quigg, J., ‘Maximal coactions’, preprint, 2000.Google Scholar
[2]Echterhoff, S., Kaliszewski, S., Quigg, J. and Raeburn, I., ‘Naturality and induced representations’, Bull. Austral. Math. Soc. 61 (2000), 415–438.CrossRefGoogle Scholar
[3]Echterhoff, S. and Quigg, J., ‘Full duality for coactions of discrete groups’, Math. Scand., to appear.Google Scholar
[4]Echterhoff, S. and Quigg, J., ‘Induced coactions of discrete groups on C*-algebras’, Canad. J. Math. 51 (1999), 745–770.CrossRefGoogle Scholar
[5]Echterhoff, S. and Raeburn, I., ‘Multipliers of imprimitivity bimodules and Morita equivalence of crossed products’, Math. Scand. 76 (1995), 289–309.Google Scholar
[6]Green, P., ‘The local structure of twisted covanance algebras’, Acta Math. 140 (1978), 191–250.Google Scholar
[7]Kaliszewski, S. and Quigg, J., ‘Imprimitivity for C*-coactions of non-amenable groups’, Math. Proc. Cambridge Philos. Soc. 123 (1998), 101–118.Google Scholar
[8]Kaliszewski, S., Quigg, J. and Raeburn, I., ‘Duality of restriction and induction for C*-coactions’, Trans. Amer. Math. Soc. 349 (1997), 2085–2113.Google Scholar
[9]Katayama, Y., ‘Takesaki's duality for a non-degenerate co-action’, Math. Scand. 55 (1985), 141–151.CrossRefGoogle Scholar
[10]Landstad, M. B., Phillips, J., Raeburn, I. and Sutherland, C. E., ‘Representations of crossed products by coactions and principal bundles’, Trans. Amer Math. Soc. 299 (1987), 747–784.Google Scholar
[11]Mansfield, K., ‘Induced representations of crossed products by coactions’, J. Funct. Anal. 97 (1991), 112–161.Google Scholar
[12]Ng, C. K., ‘A remark on Mansfield's imprimitivity theorem’, Proc. Amer. Math. Soc. 126 (1998), 3767–3768.Google Scholar
[13]Phillips, J. and Raeburn, I., ‘Twisted crossed products by coactions’, J. Austral. Math. Soc. Ser A 56 (1994), 320–344.Google Scholar
[14]Quigg, J., ‘Full and reduced C*-coactions, Math. Proc. Cambridge Philos. Soc. 116 (1994), 435–450.CrossRefGoogle Scholar
[15]Quigg, J. and Raeburn, I., ‘Induced C*-algebras and Landstad duality for twisted coactions’, Trans. Amer Math. Soc. 347 (1995), 2885–2915.Google Scholar
[16]Raeburn, I., ‘On crossed products by coactions and their representation theory’, Proc. London Math. Soc. 64 (1992), 625–652.Google Scholar
[17]Sieben, N., ‘Morita equivalence of C*-crossed products by inverse semigroup actions’, Rocky Mountain J. Math., to appear.Google Scholar
You have
Access