Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-23T15:04:06.316Z Has data issue: false hasContentIssue false
  • English
  • Français

Three additive congruences to a large prime modulus

Part of: Diophantine equations

Published online by Cambridge University Press:  09 April 2009

O. D. Atkinson ,
J. Brüdern  and
R. J. Cook
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let k ≥ 3 and n > 6k be positive integers. The equations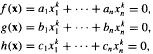, with integer coefficients, have nontrivial p-adic solutions for all p > Ck8, where C is some positive constant. Further, for values k≥ K we can take C = 1 + O(K-½).

MSC classification

Secondary: 11D88: $p$-adic and power series fields
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 55 , Issue 3 , December 1993 , pp. 355 - 368
Copyright
Copyright © Australian Mathematical Society 1993

References

Aigner, M. (1979), Combinatorial Theory, (Springer, Berlin).CrossRefGoogle Scholar
Atkinson, O. D. and Cook, R. J. (1989), ‘Pairs of additive congruences to a large prime modulus’, J. Austral. Math. Soc. Series A 46, 438–455.CrossRefGoogle Scholar
Davenport, H. (1963), Analytic met hods for Diophantine equations and Diophantine inequalities, (Campus Publishers, Ann Arbor).Google Scholar
Davenport, H. and Lewis, D. J. (1969), ‘Simultaneous equations of additive type’, Philos. Trans. Roy. Soc. London Ser. A 264, 577–595.Google Scholar
Dodson, M. M. (1966), ‘Homogeneous additive congruences’, Philos. Trans. Roy. Soc. London Ser. A 261, 163–210.Google Scholar
Dörmer, E. (1990), ‘Simultaneous diagonal equations over certain p-adic fields’,J. Number Theory 36, 1–11.Google Scholar
Ellison, F. (1973), ‘Three diagonal quadratic forms’,Acta Arith. 23, 137–151.CrossRefGoogle Scholar
Low, L., Pitman, J. and Wolff, A. (1988), ‘Simultaneous diagonal congruences’, J. Number Theory 29, 31–59.CrossRefGoogle Scholar
Schmid, W. M. (1984), ‘The solubility of certain p-adic equations’, J. Number Theory 19, 63–80.CrossRefGoogle Scholar
Wooley, T. D. (1990), ‘On simultaneous additive equations III’, Mathematika 37, 85–96.CrossRefGoogle Scholar