Hostname: page-component-745bb68f8f-kw2vx Total loading time: 0 Render date: 2025-01-11T03:26:25.434Z Has data issue: false hasContentIssue false
  • English
  • Français

A theorem on a finite difference operator and its connection with the Poisson distribution

Published online by Cambridge University Press:  09 April 2009

Q. A. M. M. Yahya
Q. A. M. M. Yahya
Affiliation:
University of DaccaEast Pakistan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The well-known Taylor expansion of a function around a point a can be formally written as 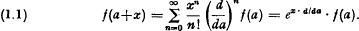The last expression is just a symbolic form and is valid, as we know, under certain restrictive conditons. The last expression is just a symbolic form and is valid, as we know, under certain restrictive conditons. We shall study the situation when the differential operator d/da is replaced by the finite difference operator Δh/h, where the operator Δh, is defined by 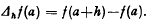In general, 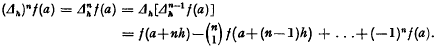Then we have the following theorem.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 6 , Issue 1 , February 1966 , pp. 25 - 29
Copyright
Copyright © Australian Mathematical Society 1966

References

[1]Bernstein, S., “Démonstration du théoréme de Weierstrass fondée sur le calcul des probabilités”, Communic. Soc. Math. Cracow, vol. 13, p. 1.Google Scholar
[2]Cramér, H., Mathematical methods of statistics, Princeton University Press, Princeton.Google Scholar
[3]Hille, E. and Phillips, R. S., Functional analysis and semi-groups, Amer. Math. Soc. Colloquium Publications, vol. XXXI, 1957.Google Scholar