Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-23T23:27:01.529Z Has data issue: false hasContentIssue false
  • English
  • Français

TENSOR-PRODUCT COACTION FUNCTORS

Part of: Selfadjoint operator algebras Methods of category theory in functional analysis

Published online by Cambridge University Press:  24 March 2020

S. KALISZEWSKI Open the ORCID record for S. KALISZEWSKI [Opens in a new window] ,
MAGNUS B. LANDSTAD  and
JOHN QUIGG
S. KALISZEWSKI
Affiliation:
School of Mathematical & Statistical Sciences, Arizona State University, Tempe, AZ 85287, USA e-mail: [email protected]
MAGNUS B. LANDSTAD
Affiliation:
Department of Mathematical Sciences, Norwegian University of Science & Technology, NO-7491 Trondheim, Norway e-mail: [email protected]
JOHN QUIGG
Affiliation:
School of Mathematical & Statistical Sciences, Arizona State University, Tempe, AZ 85287, USA e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Recent work by Baum et al. [‘Expanders, exact crossed products, and the Baum–Connes conjecture’, Ann. K-Theory 1(2) (2016), 155–208], further developed by Buss et al. [‘Exotic crossed products and the Baum–Connes conjecture’, J. reine angew. Math. 740 (2018), 111–159], introduced a crossed-product functor that involves tensoring an action with a fixed action 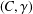$(C,\unicode[STIX]{x1D6FE})$, then forming the image inside the crossed product of the maximal-tensor-product action. For discrete groups, we give an analogue for coaction functors. We prove that composing our tensor-product coaction functor with the full crossed product of an action reproduces their tensor-crossed-product functor. We prove that every such tensor-product coaction functor is exact, and if 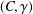$(C,\unicode[STIX]{x1D6FE})$ is the action by translation on 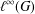$\ell ^{\infty }(G)$, we prove that the associated tensor-product coaction functor is minimal, thereby recovering the analogous result by the above authors. Finally, we discuss the connection with the 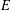$E$-ization functor we defined earlier, where 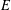$E$ is a large ideal of 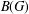$B(G)$.

Keywords

crossed productactioncoactiontensor productFell bundle

MSC classification

Primary: 46L55: Noncommutative dynamical systems
Secondary: 46M15: Categories, functors
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 112 , Issue 1 , February 2022 , pp. 52 - 67
Check for updates
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Communicated by L. O. Clark

Dedicated to the memory of J. M. G. Fell, 1923–2016

References

Abadie-Vicens, F., ‘Tensor products of Fell bundles over discrete groups’, Preprint, 1997, arXiv:funct-an/9712006.Google Scholar
Ara, P., Exel, R. and Katsura, R., ‘Dynamical systems of type (m, n) and their C ∗ -algebras’, Ergodic Theory Dynam. Systems 33(5) (2013), 1291–1325.CrossRefGoogle Scholar
Baum, P., Guentner, E. and Willett, R., ‘Expanders, exact crossed products, and the Baum–Connes conjecture’, Ann. K-Theory 1(2) (2016), 155–208.CrossRefGoogle Scholar
Buss, A., Echterhoff, S. and Willett, R., ‘Exotic crossed products and the Baum–Connes conjecture’, J. reine angew. Math. 740 (2018), 111–159.CrossRefGoogle Scholar
Echterhoff, S., Kaliszewski, S. and Quigg, J., ‘Maximal coactions’, Internat. J. Math. 15 (2004), 47–61.CrossRefGoogle Scholar
Echterhoff, S., Kaliszewski, S., Quigg, J. and Raeburn, I., A Categorical Approach to Imprimitivity Theorems for C ∗ -Dynamical Systems, Vol. 180, Memoirs of the American Mathematical Society, 850 (American Mathematical Society, Providence, RI, 2006).Google Scholar
Exel, R., Partial Dynamical Systems, Fell Bundles and Applications, Mathematical Surveys and Monographs, 224 (American Mathematical Society, Providence, RI, 2017).CrossRefGoogle Scholar
Fell, J. M. G. and Doran, R. S., Representations of *-Algebras, Locally Compact Groups, and Banach *-Algebraic Bundles. Vol. 2, Pure and Applied Mathematics, 126 (Academic Press, Boston, MA, 1988).Google Scholar
Kaliszewski, S., Landstad, M. B. and Quigg, J., ‘Coaction functors’, Pacific J. Math. 284(1) (2016), 147–190.CrossRefGoogle Scholar
Kaliszewski, S., Landstad, M. B. and Quigg, J., ‘Coaction functors, II’, Pacific J. Math. 293(2) (2018), 301–339.CrossRefGoogle Scholar
Ng, C.-K., ‘Discrete coactions on C ∗ -algebras’, J. Aust. Math. Soc. Ser. A 60(1) (1996), 118–127.Google Scholar
Quigg, J. C., ‘Discrete C ∗ -coactions and C ∗ -algebraic bundles’, J. Aust. Math. Soc. Ser. A 60 (1996), 204–221.Google Scholar