Hostname: page-component-6bf8c574d5-xtvcr Total loading time: 0 Render date: 2025-02-16T20:08:37.688Z Has data issue: false hasContentIssue false
  • English
  • Français

SYSTEMS OF ISLANDS WITH CONTINUOUS HEIGHT FUNCTIONS

Part of: Combinatorics Real functions

Published online by Cambridge University Press:  01 May 2013

ZSOLT LENGVÁRSZKY
ZSOLT LENGVÁRSZKY*
Affiliation:
Department of Mathematics, Louisiana State University Shreveport, 1 University Place, Shreveport, LA 71115, USA
*
[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We investigate island systems with continuous height functions and strongly laminar systems which are laminar systems containing sets with disjoint boundaries. In the discrete case, we show that for a maximal rectangular system of islands 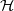$ \mathcal{H} $ on an 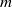$m$ by $n$ rectangular grid we have 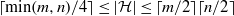$\lceil \min (m, n)/ 4\rceil \leq \vert \mathcal{H} \vert \leq \lceil m/ 2\rceil \lceil n/ 2\rceil $. In the continuous case we show that under some conditions maximal strongly laminar systems 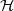$ \mathcal{H} $ have cardinality 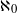${\aleph }_{0} $ or 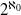${2}^{{\aleph }_{0} } $ and present examples with 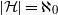$\vert \mathcal{H} \vert = {\aleph }_{0} $.

Keywords

systems of islandscontinuous height functionsstrongly laminar systems

MSC classification

Secondary: 05A05: Permutations, words, matrices 05A16: Asymptotic enumeration 26A03: Foundations 26A30: Singular functions, Cantor functions, functions with other special properties
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 94 , Issue 3 , June 2013 , pp. 385 - 396
Copyright
Copyright ©2013 Australian Mathematical Publishing Association Inc. 

References

Baráth, J., Hajnal, P. and Horváth, E. K., ‘Elementary proof techniques for the maximum number of islands’, European J. Combin. 32 (2011), 276–281.CrossRefGoogle Scholar
Czédli, G., ‘The number of rectangular islands by means of distributive lattices’, European J. Combin. 30 (2009), 208–215.CrossRefGoogle Scholar
Czédli, G., Huhn, A. P. and Schmidt, E. T., ‘Weakly independent subsets in lattices’, Algebra Universalis 20 (1985), 194–196.CrossRefGoogle Scholar
Földes, S. and Singhi, N. M., ‘On instantaneous codes’, J. Comb. Inf. Syst. Sci. 31 (2006), 317–326.Google Scholar
Horváth, E. K., Horváth, G., Németh, Z. and Szabó, Cs., ‘The number of square islands on a rectangular sea’, Acta Sci. Math. (Szeged) 76 (2010), 35–48.CrossRefGoogle Scholar
Horváth, E. K., Németh, Z. and Pluhár, G., ‘The number of triangular islands on a triangular grid’, Period. Math. Hungar. 58 (2009), 25–34.CrossRefGoogle Scholar
Horváth, E. K., Šešelja, B. and Tepavčević, A., ‘Cut approach to islands in rectangular fuzzy relations’, Fuzzy Sets and Systems 161 (2010), 3114–3126.CrossRefGoogle Scholar
Lengvárszky, Zs., ‘The minimum cardinality of maximal systems of rectangular islands’, European J. Combin. 30 (2009), 216–219.CrossRefGoogle Scholar
Lengvárszky, Zs., ‘The size of maximal systems of square islands’, European J. Combin. 30 (2009), 889–892.CrossRefGoogle Scholar
Lengvárszky, Zs., ‘Notes on triangular islands’, Acta Sci. Math. (Szeged) 75 (2009), 369–376.Google Scholar
Lengvárszky, Zs. and Pach, P. P., ‘A note on systems of rectangular islands: the continuous case’, Acta Sci. Math. (Szeged) 77 (2011), 27–34.CrossRefGoogle Scholar
Máder, A. and Makay, G., ‘The maximum number of rectangular islands’, The Teaching of Math. 14 (2011), 31–44.Google Scholar
Pach, P. P., Pluhár, G., Pongrácz, A. and Szabó, Cs., ‘The possible number of islands on the sea’, J. Math. Anal. Appl. 375 (2011), 8–13.CrossRefGoogle Scholar
Pluhár, G., ‘The number of brick islands by means of distributive lattices’, Acta Sci. Math. (Szeged) 75 (2009), 3–11.Google Scholar
Thim, J., ‘Continuous nowhere differentiable functions’, Master’s Thesis, Luleå University of Technology, 2003.Google Scholar