Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-23T14:21:23.633Z Has data issue: false hasContentIssue false
  • English
  • Français

Systems of derivations on topological algebras of power series

Published online by Cambridge University Press:  09 April 2009

Henry J. Schultz
Henry J. Schultz
Affiliation:
Claremont Graduate SchoolClaremont, California 91711, U.S.A.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

If Do, D1, … are linear maps from an algebra A to an algebra B, both over the complexes, then {Do, D1, …} is a system of derivations if for all a, b in A and for all nonnegative integers k, we have 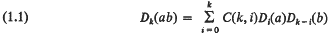Where C(k, i) is the binomial coefficient k!/i! (k—i)!. By (1.1) we see that Do must be a homomorphism and in case Do = I, where I is the identity map, D1 is a derivation and, for k ≧ 2, the Dk are higher derivations in the sense of Jacobson (1964), page 191. Gulick (1970), Theorem 4.2, proved that if A is a commutative regular semi-simple F-algebra with identity and {DO, D1, …} is a system of derivations from A to B = C(S(A)), the algebra of all continuous functions on the spectrum of A, where Dox = x, then the Dk are all continuous. Carpenter (1971), Theorem 5, shows that the regularity condition is unnecessary and Loy (1973) generalizes this a bit further. One of the many interesting features of systems of derivations is that they help determine analytic structure in Banach algebras (see for example, Miller (to appear)).

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 19 , Issue 3 , May 1975 , pp. 358 - 370
Copyright
Copyright © Australian Mathematical Society 1975

References

Carpenter, R. L. (1971), ‘Continuity of systems of derivations on F-algebras’, Proc. Amer. Math. Soc. 30, 141–146.Google Scholar
Grabiner, S. (1967), Radical Banach algebras and formal power series, thesis, (Harvard, 1967).Google Scholar
Grabiner, S. (1971), ‘A formal power series operational calculus for quasi-nilpotent operations’, Duke Math. J. 38, 641–658.CrossRefGoogle Scholar
Grabiner, S. (1973), ‘A formal power series operational calculus for quasi-nilpotent operations II’, J. Math. Anal. Appl. 43, 170–192.CrossRefGoogle Scholar
Grabiner, S. (1974), ‘Derivations and automorphisms of Banach algebras of power series’, Mem. Amer. Math. Soc. 146.Google Scholar
Grabiner, S. (to appear), ‘Weighted shifts and Banach algebras of power series’, Amer. J. Math.Google Scholar
Gulick, F. (1970), ‘Systems of derivations’, Trans. Amer. Math. Soc. 149, 465–488.CrossRefGoogle Scholar
Jacobson, N. (1964), Lectures in abstract algebra Vol. 3, Theory of fields and Galois theory, (Van Nostrand, Princeton, N. J. 1964).Google Scholar
Johnson, B. E. (1967), ‘Continuity of linear operators commuting with continuous linear operators’, Trans. Amer. Math. Soc. 128, 88–102.CrossRefGoogle Scholar
Johnson, B. E. (1969), ‘Continuity of derviations on commutative algebras’, Amer. J. Math. 91, 1–10.CrossRefGoogle Scholar
Loy, R. J. (1969), ‘Continuity of derivations on topological algebras of power series’, Bull, Austral. Math. Soc. 1, 419–442.CrossRefGoogle Scholar
Loy, R. J. (1970), ‘Uniqueness of the complete norm topology and continuity of derivations of Banach algebras’, Tohoku Math. J. 22, 371–378.CrossRefGoogle Scholar
Loy, R. J. (1971), ‘Uniqueness of the Frechet space topology on certain topological algebras’, Bull. Austral. Math. S:c. 4, 1–7.CrossRefGoogle Scholar
Loy, R. J. (1973), ‘Continuity of higher derivations’, Proc. Amer. Math. Soc. 37, 505–510.CrossRefGoogle Scholar
Loy, R. J. (preprint), ‘Banach algebras of power series’.Google Scholar
Miller, J. B. (1970), ‘Higher derivations on Banach algebras’, Amer. J. Math. 92, 301–333.CrossRefGoogle Scholar
Miller, J. B. (to appear), ‘Analytic structure and higher derivations on commutative Banach algebras’, Aequationes Mathematicae.Google Scholar
Scheinberg, S. (1970), ‘Power series in one variable’, J. Math. Anal. Appl. 31, 321–333.CrossRefGoogle Scholar
Wilansky, A. (1964), Functional Analysis, (Blaisdell, New York 1964).Google Scholar