A graph 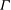$\Gamma $ is 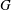$G$-symmetric if 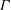$\Gamma $ admits 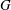$G$ as a group of automorphisms acting transitively on the set of vertices and the set of arcs of 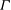$\Gamma $, where an arc is an ordered pair of adjacent vertices. In the case when 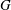$G$ is imprimitive on 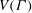$V(\Gamma )$, namely when 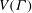$V(\Gamma )$ admits a nontrivial 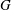$G$-invariant partition 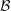${\mathcal{B}}$, the quotient graph 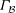$\Gamma _{\mathcal{B}}$ of 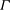$\Gamma $ with respect to 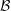${\mathcal{B}}$ is always 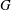$G$-symmetric and sometimes even 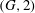$(G, 2)$-arc transitive. (A 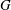$G$-symmetric graph is 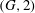$(G, 2)$-arc transitive if 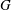$G$ is transitive on the set of oriented paths of length two.) In this paper we obtain necessary conditions for 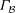$\Gamma _{{\mathcal{B}}}$ to be 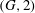$(G, 2)$-arc transitive (regardless of whether 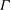$\Gamma $ is 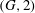$(G, 2)$-arc transitive) in the case when 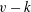$v-k$ is an odd prime 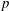$p$, where $v$ is the block size of 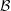${\mathcal{B}}$ and 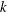$k$ is the number of vertices in a block having neighbours in a fixed adjacent block. These conditions are given in terms of 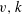$v, k$ and two other parameters with respect to 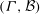$(\Gamma , {\mathcal{B}})$ together with a certain 2-point transitive block design induced by 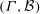$(\Gamma , {\mathcal{B}})$. We prove further that if 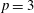$p=3$ or 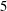$5$ then these necessary conditions are essentially sufficient for 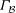$\Gamma _{{\mathcal{B}}}$ to be 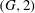$(G, 2)$-arc transitive.