Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Moran, P. A. P.
1961.
The survival of a mutant under general conditions.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 57,
Issue. 2,
p.
304.
Pollak, Edward
1966.
On the survival of a gene in a subdivided population.
Journal of Applied Probability,
Vol. 3,
Issue. 1,
p.
142.
Pollak, Edward
1966.
On the survival of a gene in a subdivided population.
Journal of Applied Probability,
Vol. 3,
Issue. 01,
p.
142.
Daley, D. J.
1968.
Stochastically monotone Markov Chains.
Zeitschrift f�r Wahrscheinlichkeitstheorie und Verwandte Gebiete,
Vol. 10,
Issue. 4,
p.
305.
Arnold, Barry C.
1968.
A modification of a result due to Moran.
Journal of Applied Probability,
Vol. 5,
Issue. 1,
p.
220.
Arnold, Barry C.
1968.
A modification of a result due to Moran.
Journal of Applied Probability,
Vol. 5,
Issue. 01,
p.
220.
Daley, D. J.
and
Moran, P. A. P.
1968.
Two-Sided Inequalities for Waiting Time and Queue Size Distributions in $GI/G/1$.
Theory of Probability & Its Applications,
Vol. 13,
Issue. 2,
p.
338.
Schaffer, H. E.
1970.
Mathematical Topics in Population Genetics.
p.
317.
Heyde, C.C.
1977.
The effect of selection on genetic balance when the population size is varying.
Theoretical Population Biology,
Vol. 11,
Issue. 2,
p.
249.
Buckley, M. J.
and
Seneta, E.
1983.
On Arnold's treatment of Moran's bounds.
Advances in Applied Probability,
Vol. 15,
Issue. 1,
p.
212.
Buckley, M. J.
and
Seneta, E.
1983.
On Arnold's treatment of Moran's bounds.
Advances in Applied Probability,
Vol. 15,
Issue. 1,
p.
212.
Nagylaki, Thomas
1985.
Biased intrachromosomal gene conversion in a chromosome lineage.
Journal of Mathematical Biology,
Vol. 21,
Issue. 3,
p.
215.
Schuster, Peter
and
Sigmund, Karl
1989.
Fixation probabilities for advantageous mutants: a note on multiplication and sampling.
Mathematical Biosciences,
Vol. 95,
Issue. 1,
p.
37.
Athreya, K. B.
1992.
Rates of decay for the survival probability of a mutant gene.
Journal of Mathematical Biology,
Vol. 30,
Issue. 6,
p.
577.
Hoppe, Fred M.
1992.
Asymptotic rates of growth of the extinction probability of a mutant gene.
Journal of Mathematical Biology,
Vol. 30,
Issue. 6,
p.
547.
B�rger, Reinhard
and
Ewens, Warren J.
1995.
Fixation probabilities of additive alleles in diploid populations.
Journal of Mathematical Biology,
Vol. 33,
Issue. 5,
p.
557.
Martin, Clyde F.
Hanlon, Bret
and
Zhou, Yishao
2005.
Extinction of genotypes in closed populations.
Proceedings of the ISCIE International Symposium on Stochastic Systems Theory and its Applications,
Vol. 2005,
Issue. 0,
p.
1.
Lambert, Amaury
2006.
Probability of fixation under weak selection: A branching process unifying approach.
Theoretical Population Biology,
Vol. 69,
Issue. 4,
p.
419.
Patwa, Z
and
Wahl, L.M
2008.
The fixation probability of beneficial mutations.
Journal of The Royal Society Interface,
Vol. 5,
Issue. 28,
p.
1279.
Rice, Daniel P
and
Townsend, Jeffrey P
2012.
A Test for Selection Employing Quantitative Trait Locus and Mutation Accumulation Data.
Genetics,
Vol. 190,
Issue. 4,
p.
1533.
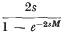 so long as s2M is small. This also holds when s is small and negative.
so long as s2M is small. This also holds when s is small and negative.