Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-23T14:13:12.524Z Has data issue: false hasContentIssue false
  • English
  • Français

Sufficient conditions for the strong stability of the differential equation [p(D)+f(t)q(D)]y = 0

Part of: Qualitative theory

Published online by Cambridge University Press:  09 April 2009

A. Howe
A. Howe
Affiliation:
Department of MathematicsFaculty of Science Australian National UniversityP. O. Box 4 Canberra, ACT 2601, Australia
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A number of sufficient conditions for stability or strong stability, as used in the context of Hamiltonian systems, are found for the differential equation 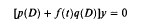where the continuous function f(t) is periodic ω in t, D = d/dt and p(s), q(s) are real monic polynomials having special properties which allow the differential equation to be transformed into a canonical system of k second order equations.

MSC classification

Secondary: 34C11: Growth, boundedness
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 47 , Issue 2 , October 1989 , pp. 280 - 299
Copyright
Copyright © Australian Mathematical Society 1989

References

[1]Brauer, Alfred and Mewborn, A. C., ‘The greatest distance between two characteristic roots of a matrix,’ Duke Math. J. 26 (1959), 653–661.Google Scholar
[2]Brockett, R. W., ‘Lie algebras and Lie groups in control theory,’ Geometric methods in system theory, edited by Mayne, D. Q. and Brockett, R. W., (Reidel, Dordrecht, Holland, 1973).Google Scholar
[3]Chiou, K. L., ‘The geometry of indefinite J-spaces and stability behaviour of linear systems,’ J. Differential Equations 28 (1978), 104–123.Google Scholar
[4]Gel'fand, I. M. and Lidskii, V. B., ‘On the structure of stability domains of linear canonical systems of differential equations with periodic coefficients,’ Uspehi Mat. Nauk 10, No. 1 (63) (1955), 3–40 (Russian);Google Scholar
Amer. Math. Soc. Transl. (2) 8 (1958), 143–181.Google Scholar
[5]Krein, M. G., ‘A generalization of some investigations of A. M. Lyapunov on linear differential equations with periodic coefficients’ Dokl. Akad. Nauk SSSR 73 (1950), 445–448 (Russian).Google Scholar
[6]Krein, M. G., ‘Fundamental aspects of the theory of λ-zone of stability for a canonical system of linear differential equations with periodic coefficients’, Pamyati A. A. Andronova, Izdat Akad. Nauk SSSR, Moscow, 1955, pp. 413–498 (Russian).Google Scholar
Translated in Krein, M. G., Topic in Differential and Integral Equations and Operator Theory: Advances and Applications, Vol. 7, Birkhauser-Verlag, Basel, 1983, pp. 1–106.CrossRefGoogle Scholar
[7]Krein, M. G., ‘On criteria for stability and boundedness of solutions of periodic canonical systems’, Prikl. Mat. Meh. 19, No. 6 (1955), 641–680 (Russian).Google Scholar
[8]Krein, M. G., ‘Introduction to the geometry of indefinite J-spaces and to the theory of operators in those spaces’, Second Math. Summer School, Part I, Naukova Dumka, Kiev, 1965, pp. 15–92 (Russian);Google Scholar
Amer. Math. Soc. Transl. (2) 93 (1970), 177–200.Google Scholar
[9]Marshall, A. W. and Olkin, I., Inequalities: Theory of majorization and its applications, (Academic Press, New York, 1979).Google Scholar
[10]Mirsky, L., ‘The spread of a matrix’, Mathematika 3 (1956), 127–130.CrossRefGoogle Scholar
[11]Neigauz, M. G. and Lidskii, V. B., ‘On the boundedness of the solutions of linear systems of differential equations with periodic coefficients’. Dokl. Akad. Nauk SSSR (N.S.) 77 (1951), 189–192 (Russian).Google Scholar
[12]Wolkowicz, Henry and Styan, George P. H., ‘Bounds for eigenvalues using traces,’ Linear Algebra and Appl. 29 (1980), 471–506.CrossRefGoogle Scholar
[13]Yakubovich, V. A., ‘Questions of the stability of solutions of a system of two linear differential equations of canonical form with periodic coefficients’, Mat. Sb. (N.S.) 37 (1955), 21–68. (Russian).Google Scholar
[14]Yakubovich, V. A., ‘On convex properties of stability regions of linear Hamiltonian systems of differential equations with periodic coefficients,’ Vestnik Leningrad Univ. Math. 17 (1962), 61–86 (Russian).Google Scholar
[15]Yakubovich, V. A. and Starzhinskii, V. M., Linear differential equations with periodic coefficients. (Nauka, Moscow, 1972) (Russian). Transl. (Keter Publishing House Jerusalem Ltd., 1975).Google Scholar
[16]Zhukovskii, N. E., ‘Finiteness conditions for integrals of the equation d 2y/dx 2 + py = 0,’ Mat. Sb. 16, No. 3 (1882), 582–591 (Russian).Google Scholar