Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-05T06:58:56.087Z Has data issue: false hasContentIssue false
  • English
  • Français

Subelliptic operators on Lie groups: regularity

Part of: Abstract harmonic analysis Approximations and expansions Lie groups

Published online by Cambridge University Press:  09 April 2009

A. F. M. Ter Elst  and
Derek W. Robinson
A. F. M. Ter Elst
Affiliation:
Centre for Mathematics and its Applications, School of Mathematical Sciences, Australian National University, ACT 0200, Australia
Derek W. Robinson
Affiliation:
Centre for Mathematics and its Applications, School of Mathematical Sciences, Australian National University, ACT 0200, Australia
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let (ℋ, G, U) be a continuous representation of the Lie group G by bounded operators g ↦ U(g) on the Banach space ℋ and let (ℋ, g, dU) denote the representation of the Lie algebra g obtained by differentiation. If a1,…, ad′ is a Lie algebra basis of g and Ai = dU(ai) then we examine elliptic regularity properties of the subelliptic operators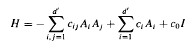 where (cij) is a real-valued strictly positive-definite matrix and c0, c1,…, cd′ ∈ C. We first introduce a family of Lipschitz subspaces ℋγ, γ > 0, of ℋ which interpolate between the Cn-subspaces of the representation and for which the parameter γ is a continuous measure of differentiability. Secondly, we give a variety of characterizations of the spaces in terms of the semigroup generated by the closure 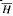of H and the group representation. Thirdly, for sufficiently large values of Re c0 the fractional powers of the closure of H are defined, and we prove that D(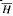)γ⊆γ′, for γ′ < 2γ/r where r is the rank of the basis. Further we establish that 2γ/r is the optimal regularity value and it is attained for unitary representations or for the representations obtained by restricting U to ℋγ. Many other regularity properties are obtained.

MSC classification

Secondary: 43A65: Representations of groups, semigroups, etc. 41A05: Interpolation 22E45: Representations of Lie and linear algebraic groups over real fields
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 57 , Issue 2 , October 1994 , pp. 179 - 229
Copyright
Copyright © Australian Mathematical Society 1994

References

[1]Beals, R. and Greiner, P., Calculus on Heisenberg manifolds, Ann. of Math. Stud. 119 (Princeton University Press, Princeton, 1988).CrossRefGoogle Scholar
[2]Bratteli, O., Goodman, F. M., Jørgensen, P. E. T. and Robinson, D. W., ‘Unitary representations of Lie groups and Gårding's inequality’, Proc. Amer. Math. Soc. 107 (1989), 627–632.Google Scholar
[3]Bratteli, O. and Robinson, D. W., Operator algebras and quantum statistical mechanics, I, 2nd edition (Springer, New York, 1987).CrossRefGoogle Scholar
[4]Burns, R. J., ter Elst, A. F. M. and Robinson, D. W., ‘Lp-regularity of subelliptic operators on Lie groups’, J. Operator Theory, to appear.Google Scholar
[5]Burns, R. J. and Robinson, D. W., ‘A priori inequalities on Lie groups’, Research Report SMS-023-90, (The Australian National University, 1990).Google Scholar
[6]Butzer, P. L. and Berens, H., Semi-groups of operators and approximation, Grundlehren Math. Wiss. 145 (Springer, Berlin, 1967).CrossRefGoogle Scholar
[7]ter Elst, A. F. M., ‘On the differential structure of principal series representations’, J. Operator Theory 28 (1992), 309–320.Google Scholar
[8]Goodman, R., ‘Analytic domination by fractional powers of a positive operator’, J. Funct. Anal. 3 (1969), 246–264.CrossRefGoogle Scholar
[9]Goodman, R. and Wallach, N. R., ‘Whittaker vectors and conical vectors’, J. Funct. Anal. 39 (1980), 199–279.CrossRefGoogle Scholar
[10]Jerison, D. S. and Sánchez-Calle, A., ‘Estimates for the heat kernel for a sum of squares of vector fields’, Indiana Univ. Math. J. 35 (1986), 835–854.CrossRefGoogle Scholar
[11]Jøgensen, P. E. T., ‘Representations of differential operators on a Lie group’, J. Funct. Anal. 20 (1975), 105–135.CrossRefGoogle Scholar
[12]Kato, T., ‘A generalization of the Heinz inequality’, Proc. Japan Acad. Ser. A Math. Sci. 37 (1961), 305–308.CrossRefGoogle Scholar
[13]Kato, T., Perturbation theory for linear operators, Grundlehren Math. Wiss. 132, 2nd edition (Springer-Verlag, Berlin, 1984).Google Scholar
[14]Nagel, A., Stein, E. M. and Wainger, S., ‘Balls and metrics defined by vector fields I:basic properties’, Acta Math. 155 (1985), 103–147.CrossRefGoogle Scholar
[15]Nelson, E., ‘Analytic vectors’, Ann. of Math. (2) 70 (1959), 572–615.CrossRefGoogle Scholar
[16]Pesenson, I. Z., ‘On interpolation spaces on Lie groups’, Soviet Math. Dokl. 20 (1979), 611–616.Google Scholar
[17]Pesenson, I. Z., ‘Nikol'ski–Besov spaces connected with representations of Lie groups’, Soviet Math.Dokl. 28 (1983), 577–581.Google Scholar
[18]Pesenson, I. Z., ‘On an abstract theory of Nikol'ski-Besov spaces’, Soviet Math. (lz. VUZ) 32 (1988), 80–92. Izv. Vyssh. Uchebn. Zaved. Mat. 32, (1988), 59–68.Google Scholar
[19]Poulsen, N. S., ‘On C ∞-vectors and intertwining bilinear forms for representations of Lie groups’, J. Funct. Anal. 9 (1972), 87–120.CrossRefGoogle Scholar
[20]Robinson, D. W., ‘Lie groups and Lipschitz spaces’, Duke Math. J. 57 (1988), 357–395.CrossRefGoogle Scholar
[21]Robinson, D. W., ‘Commutators and generators II’, Math. Scand. 64 (1989), 87–108.CrossRefGoogle Scholar
[22]Robinson, D. W., Elliptic operators and Lie groups, Oxford Math. Monographs (Oxford University Press, Oxford, 1991).CrossRefGoogle Scholar
[23]Rothschild, L. P. and Stein, E. M., ‘Hypoelliptic differential operators and nilpotent groups’, Acta Math. 137 (1976), 247–320.CrossRefGoogle Scholar
[24]Stein, E. M., Singular integrals and differential properties of functions, Princeton Math. Ser. 30 (Princeton University Press, Princeton, 1970).Google Scholar
[25]Triebel, H., Interpolation theory, function spaces, differential operators (North-Holland, Amsterdam, 1978).Google Scholar
[26]Varopoulos, N. T., ‘Analysis on Lie groups’, J. Funct. Anal. 76 (1988), 346–410.CrossRefGoogle Scholar
[27]Varopoulos, N. T., Saloff-Coste, L. and Coulhon, T., Analysis and geometry on groups, Cambridge Tracts in Mathematics 100 (Cambridge University Press, Cambridge, 1992).Google Scholar
[28]Zygmund, A., Trigonometric series II, 2nd edition (Cambridge University Press, Cambridge, 1959).Google Scholar