Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-22T22:11:56.533Z Has data issue: false hasContentIssue false
  • English
  • Français

STRUCTURE THEOREM FOR 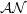$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathcal{AN}$-OPERATORS

Part of: General theory of linear operators

Published online by Cambridge University Press:  30 April 2014

G. RAMESH
G. RAMESH*
Affiliation:
Department of Mathematics, Indian Institute of Technology Hyderabad, Ordnance Factory Estate, Yeddumailaram 502 205, Andhra Pradesh, India email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we prove a structure theorem for the class of 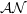$\mathcal{AN}$-operators between separable, complex Hilbert spaces which is similar to that of the singular value decomposition of a compact operator. Apart from this, we show that a bounded operator is 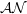$\mathcal{AN}$ if and only if it is either compact or a sum of a compact operator and scalar multiple of an isometry satisfying some condition. We obtain characterizations of these operators as a consequence of this structure theorem and deduce several properties which are similar to those of compact operators.

Keywords

-operatorcompact operatorisometryminimum modulus

MSC classification

Secondary: 47A75: Eigenvalue problems 47A10: Spectrum, resolvent
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 96 , Issue 3 , June 2014 , pp. 386 - 395
Copyright
Copyright © 2014 Australian Mathematical Publishing Association Inc. 

References

Bakić, D., ‘Compact operators, the essential spectrum and the essential numerical range’, Math. Commun. 3(1) (1998), 103–108.Google Scholar
Carvajal, X. and Neves, W., ‘Operators that achieve the norm’, Integral Equations Operator Theory 72(2) (2012), 179–195.CrossRefGoogle Scholar
Conway, J. B., A Course in Functional Analysis, Graduate Texts in Mathematics, 96, 2nd edn (Springer, New York, 1990).Google Scholar
Douglas, R. G., Banach Algebra Techniques in Operator Theory, Pure and Applied Mathematics, 49 (Academic Press, New York, 1972).Google Scholar
Fillmore, P. A., Stampfli, J. G. and Williams, J. P., ‘On the essential numerical range, the essential spectrum, and a problem of Halmos’, Acta Sci. Math. (Szeged) 33 (1972), 179–192.Google Scholar
Gohberg, I., Goldberg, S. and Kaashoek, M. A., Basic Classes of Linear Operators (Birkhäuser Verlag, Basel, 2003).Google Scholar
Halmos, P. R., A Hilbert Space Problem Book, Graduate Texts in Mathematics, 19, 2nd edn (Springer, New York, 1982).CrossRefGoogle Scholar
Kato, T., Perturbation Theory for Linear Operators, Classics in Mathematics, Reprint of the 1980 edition (Springer, Berlin, 1995).CrossRefGoogle Scholar
Ramesh, G., ‘Approximation methods for solving operator equations involving unbounded operators’, PhD Thesis, IIT Madras, 2008.Google Scholar
Retherford, J. R., Hilbert Space: Compact Operators and the Trace Theorem, London Mathematical Society Student Texts 27 (Cambridge University Press, Cambridge, 1993).CrossRefGoogle Scholar
Rudin, W., Functional Analysis, International Series in Pure and Applied Mathematics, 2nd edn (McGraw-Hill, New York, 1991).Google Scholar
Shkarin, S., ‘Norm attaining operators and pseudospectrum’, Integral Equations Operator Theory 64 (2009), 115–136.CrossRefGoogle Scholar