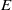Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-23T03:43:22.688Z Has data issue: false hasContentIssue false
  • English
  • Français

STRONGLY ORTHODOX CONGRUENCES ON AN $E$-INVERSIVE SEMIGROUP

Part of: Semigroups

Published online by Cambridge University Press:  01 April 2014

XINGKUI FAN  and
QIANHUA CHEN
XINGKUI FAN*
Affiliation:
School of Science, Qingdao Technological University, Qingdao, Shandong 266520, PR China School of Mathematics and Statistics, Lanzhou University, Lanzhou, Gansu 730000, PR China
QIANHUA CHEN
Affiliation:
School of Science, Qingdao Technological University, Qingdao, Shandong 266520, PR China email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we investigate some subclasses of strongly regular congruences on an 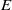$E$-inversive semigroup 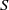$S$. We describe the minimum and the maximum strongly orthodox congruences on 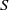$S$ whose characteristic trace coincides with the characteristic trace of given congruences and, in each case, we present an alternative characterization for them. A description of all strongly orthodox congruences on 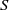$S$ with characteristic trace $\tau $ is given. Further, we investigate the kernel relation of strongly orthodox congruences on an 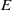$E$-inversive semigroup and give the least and the greatest element in the class of the same kernel with a given congruence.

Keywords

E-inversive semigroupsstrongly orthodox congruencecharacteristic tracekernel

MSC classification

Secondary: 20M10: General structure theory
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 96 , Issue 2 , April 2014 , pp. 216 - 230
Copyright
Copyright ©2013 Australian Mathematical Publishing Association Inc. 

References

Edwards, P. M., ‘Eventually regular semigroups’, Bull. Aust. Math. Soc. 28 (1983), 23–38.Google Scholar
Gomes, M. S., ‘The lattice of $ \mathcal{R} $-unipotent congruences on a regular semigroup’, Semigroup Forum 33 (1986), 159–173.Google Scholar
Hayes, A., ‘${E}^{\ast } $-dense $E$-semigroups’, Semigroup Forum 68 (2004), 218–232.Google Scholar
Higgins, P. M., Techniques of Semigroup Theory (Oxford University Press, Oxford, 1992).Google Scholar
Howie, J. M., Fundamentals of Semigroup Theory (Clarendon Press, Oxford, 1995).Google Scholar
LaTorre, D. R., ‘$\theta $-classes in $ \mathcal{L} $-unipotent semigroups’, Semigroup Forum 22 (1981), 355–365.Google Scholar
Luo, Y. F., Fan, X. K. and Li, X. L., ‘Regular congruences on an $E$-inversive semigroup’, Semigroup Forum 76 (2008), 107–123.CrossRefGoogle Scholar
Luo, Y. F. and Li, X. L., ‘$ \mathcal{R} $-unipotent congruences on eventually regular semigroups’, Algebra Colloq. 14 (1) (2007), 37–52.Google Scholar
Luo, Y. F. and Li, X. L., ‘Orthodox congruences on an eventually regular semigroup’, Semigroup Forum 74 (2007), 319–336.Google Scholar
Mitsch, H., ‘Subdirect products of $E$-inversive semigroups’, J. Aust. Math. Soc. 48 (1990), 66–78.Google Scholar
Mitsch, H. and Petrich, M., ‘Basic properties of $E$-inversive semigroups’, Comm. Algebra 28 (11) (2000), 5169–5182.CrossRefGoogle Scholar
Pastijn, F. and Petrich, M., ‘The congruence lattice of a regular semigroup’, J. Pure Appl. Algebra 53 (1988), 93–123.Google Scholar
Sen, M. K. and Seth, A., ‘Lattice of idempotent separating congruences in a $ \mathcal{P} $-regular semigroup’, Bull. Aust. Math. Soc. 45 (1992), 483–488.Google Scholar
Thierrin, G., ‘Sur les demi-groupes inversés’, C. R. Acad. Sci. (Paris) 234 (1952), 1336–1338.Google Scholar
Trotter, P. G. and Jiang, Z. H., ‘Covers for regular semigroups’, Southeast Asian Bull. Math. 18 (1994), 157–161.Google Scholar
Weipoltshammer, B., ‘Certain congruences on $E$-inversive $E$-semigroups’, Semigroup Forum 65 (2002), 233–248.Google Scholar
Zheng, H. W., ‘Group congruences on an $E$-inversive semigroup’, Southeast Asian Bull. Math. 21 (1997), 1–8.Google Scholar