Hostname: page-component-745bb68f8f-mzp66 Total loading time: 0 Render date: 2025-01-11T04:20:42.437Z Has data issue: false hasContentIssue false
  • English
  • Français

Stably free resolutions of lattices over finite groups

Part of: Homological algebra Representation theory of groups

Published online by Cambridge University Press:  09 April 2009

K. W. Gruenberg
K. W. Gruenberg
Affiliation:
Queen Mary and Westfield CollegeLondon, England
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For a ZG-lattice A, the nth partial free Euler characteristic εn(A) is defined as the infimum of all 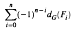where F* varies over all free resolutions of A. It is shown that there exists a stably free resolution E* of A which realises εn(A) for all n≥0 and that the function n → εn(A) is ultimately polynomial no residue classes. The existence of E* is established with the help of new invariants σn(A) of A. These are elements in certain image groups of the projective class group of ZG. When ZG allows cancellation, E* is a minimal free resolution and is essentially unique. When A is periodic, E* is ultimately periodic of period a multiple of the projective period of A.

MSC classification

Secondary: 20C10: Integral representations of finite groups 20C05: Group rings of finite groups and their modules 18G10: Resolutions; derived functors
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 49 , Issue 3 , December 1990 , pp. 364 - 385
Copyright
Copyright © Australian Mathematical Society 1990

References

[1]Bass, H., Algebraic K-theory (Benjamin, New York, 1968).Google Scholar
[2]Gruenberg, K. W., ‘Partial Euler characteristics of finite groups and the decomposition of lattices’, Proc. London Math. Soc. (3) 48 (1984), 91–107.CrossRefGoogle Scholar
[3]Gruenberg, K. W. and Linnell, P. A., ‘Minimal free resolutions of lattices over finite groups’, Illinois J. Math. 32 (1988), 361–374.CrossRefGoogle Scholar
[4]Swan, R. G., ‘Periodic resolutions for finite groups’, Ann. of Math. 72 (1960), 267–291.CrossRefGoogle Scholar
[5]Swan, R. G., ‘Minimal resolutions for finite groups’, Topology 4 (1965), 193–208.CrossRefGoogle Scholar
[6]Talelli, O., ‘On minimal resolutions for metacyclic groups with periodic cohomology’, Comm. Algebra 12 (1984), 1343–1360.CrossRefGoogle Scholar
[7]Webb, P. J., ‘Bounding the ranks of ZG-lattices by their restrictions to elementary abelian subgroups’, J. Pure Appl. Algebra 23 (1982), 311–318.CrossRefGoogle Scholar