Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-22T19:34:42.378Z Has data issue: false hasContentIssue false
  • English
  • Français

Stable perturbation in Banach algebras

Part of: Numerical analysis in abstract spaces Miscellaneous applications of functional analysis Topological algebras, normed rings and algebras, Banach algebras

Published online by Cambridge University Press:  09 April 2009

Yifeng Xue
Yifeng Xue
Affiliation:
Department of MathematicsEast China Normal UniversityShanghai [email protected], [email protected].
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

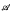Let be a unital Banach algebra. Assume that a has 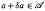a generalized inverse a+. Then is said to be a stable perturbation of a if 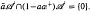. In this paper we give various conditions for stable perturbation of a generalized invertible element and show that the equation 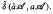is closely related to the gap function . These results will be applied to error estimates for perturbations of the Moore-Penrose inverse in C*–algebras and the Drazin inverse in Banach algebras.

MSC classification

Secondary: 46H99: None of the above, but in this section 46N40: Applications in numerical analysis 65J05: General theory
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 83 , Issue 2 , October 2007 , pp. 271 - 284
Copyright
Copyright © Australian Mathematical Society 2007

References

[1]Barnes, B. A. ‘The Fredholm elements of a ring’, Canad. J. Math. 21 (1969), 84–95.CrossRefGoogle Scholar
[2]Castro-González, N. and Koliha, J. J. ‘Perturbation of Drazin inverse for closed linear operators’, Integral Equations Operator Theory 36 (2000), 92–106.CrossRefGoogle Scholar
[3]Castro-González, N., Koliha, J. J. and Rakočević, V. ‘Continuity and general perturbation of Drazin inverse for closed linear operators’, Abstr. Appl. Anal. 7 (2002), 355–347.Google Scholar
[4]Castro-González, N., Koliha, J. J. and Wei, Y. ‘Error bounds for perturbation of the Drazin inverse of closed operators with equal spectral idempotents’, Appl. Anal. 81 (2002), 915–928.CrossRefGoogle Scholar
[5]Chen, G., Wei, M. and Xue, Y. ‘Perturbation analysis of the least squares solution in Hilbert spaces’, Linear Algebra Appl. 244 (1996), 69–80.CrossRefGoogle Scholar
[6]Chen, G. and Xue, Y. ‘Perturbation analysis for the operator equation Tx = b in Banach spaces’, J. Math. Anal. Appl. 222 (1997), 107–125.CrossRefGoogle Scholar
[7]Chen, G. and Xue, Y. ‘The expression of the generalized inverse of the perturbed operator under type I perturbation in Hilbert spaces’, Linear Algebra Appl. 285 (1998), 1–6.CrossRefGoogle Scholar
[8]Ding, J. and Huang, L. J. ‘Perturbation of generalized inverses of linear operators in Hilbert spaces’, J. Math. Anal. Appl. 198 (1996), 506–515.CrossRefGoogle Scholar
[9]Drazin, M. P. ‘Pseudo-inverses in associative rings and semigroups’, Amer. Math. Monthly 65 (1958), 506–514.CrossRefGoogle Scholar
[10]Rakočević, V. ‘Continuity of the Drazin inverse’, J. Operator Theory 41 (1999), 55–68.Google Scholar
[11]Harte, R. and Mbekhta, M., On generalized inverse in C*–algebras’, Studia Math. 103 (1992), 71–77.CrossRefGoogle Scholar
[12]Harte, R. and Mbekhta, M. ‘On generalized inverse in C*–algebras (II)’, Studia Math. 106 (1993), 129–138.CrossRefGoogle Scholar
[13]Koliha, J. J. ‘Error bounds for a general perturbation of Drazin inverse’, Appl. Math. Comput. 126 (2002), 181–185.Google Scholar
[14]Koliha, J. J. and Rakočević, V. ‘Continuity of the Drazin inverse II’, Studia Math. 131 (1998), 167–177.Google Scholar
[15]Pedersen, G. K., C*–algebras and Their Automorphism Groups (Academic Press, Boston, 1979).Google Scholar
[16]Rakočević, V. ‘On the continuity of the Moore-Penrose inverse in C*–algebras’, Math. Montisnigri 2 (1993), 89–92.Google Scholar
[17]Rakočević, V. and Wei, Y. ‘The perturbation theory for the Drazin inverse and its applications (II)’, J. Aust. Math. Soc. 70 (2001), 189–197.CrossRefGoogle Scholar
[18]Rickart, C., General Theory of Banach Algebras (Van Nostrand Reinhold, New York, 1960).Google Scholar
[19]Roch, S. and Silbermann, B. ‘Continuity of generalized inverses in Banach algebras’, Studia Math. 136 (1999), 197–227.Google Scholar
[20]Xue, Y. and Chen, G. ‘Some equivalent conditions of stable perturbation of operators in Hilbert spaces’, Applied Math. Comput. 147 (2004), 765–772.Google Scholar