No CrossRef data available.
Published online by Cambridge University Press: 09 April 2009
Nevile [2] has shown that if Rt is a certain measure of the rate of growth of the national income in Harrod's growth model of an economy, then Rt satisfies the non-linear recurrence relation 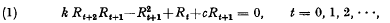 , where 0 < k < and −1 < c < 1. The definition of Rt ([2] p. 369) is such that Rt > 0 for all t. Nevile has pointed out features of the model that indicate that it may be unstable. In this paper I propose to show that the model is, in general. unstable, but that proper choice of the initial values R0R1 apparently leads to stability. In order to do this, we require the conditions (if any) under which Rt converges.
, where 0 < k < and −1 < c < 1. The definition of Rt ([2] p. 369) is such that Rt > 0 for all t. Nevile has pointed out features of the model that indicate that it may be unstable. In this paper I propose to show that the model is, in general. unstable, but that proper choice of the initial values R0R1 apparently leads to stability. In order to do this, we require the conditions (if any) under which Rt converges.