No CrossRef data available.
Article contents
Spectrality of elementary operators
Part of:
Special classes of linear operators
Published online by Cambridge University Press: 09 April 2009
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Spectrality and prespectrality of elementary operators 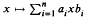 , acting on the algebra B(k) of all bounded linear operators on a separable infinite-dimensional complex Hubert space K, or on von Neumann-Schatten classes in B(k), are treated. In the case when (a1, a2, …, an) and (b1, b2, …, bn) are two n—tuples of commuting normal operators on H, the complete characterization of spectrality is given.
, acting on the algebra B(k) of all bounded linear operators on a separable infinite-dimensional complex Hubert space K, or on von Neumann-Schatten classes in B(k), are treated. In the case when (a1, a2, …, an) and (b1, b2, …, bn) are two n—tuples of commuting normal operators on H, the complete characterization of spectrality is given.
- Type
- Research Article
- Information
- Copyright
- Copyright © Australian Mathematical Society 1990
References
[1]Anderson, J. and Foiaş, C., ‘Properties which normal operators share with normal derivations and related operators’, Pacific J. Math. 61 (1975), 313–325.CrossRefGoogle Scholar
[2]Conway, J. B., Subnormal operators, (Research Notes in Mathematics 51, Pitman, Boston, London, Melbourne, 1981).Google Scholar
[3]Diestel, J. and Uhl, J. J., Vector measures, (Math. Surveys 15, Amer. Math. Soc., Providence, R. I., 1977).CrossRefGoogle Scholar
[4]Dowson, H. R., Spectral theory of linear operators, (Academic Press, London, New York, San Francisco, 1978).Google Scholar
[5]Dunford, N. and Schwartz, J. T., Linear operators, part II: Spectral theory, (Interscience, New York, London, 1963).Google Scholar
[6]Dunford, N. and Schwartz, J. T., Linear operators, part III: Spectral operators, (Wiley-Interscience, New York, London, Sydney, Toronto, 1971).Google Scholar
[7]Fialkow, L. A., ‘Spectral properties of elementary operators’, Acta Sci. Math. (Szeged) 46 (1983), 269–282.Google Scholar
[8]Fialkow, L. A., ‘Spectral properties of elementary operators II’, Transl. Amer. Math. Soc. 290 (1985), 415–429.CrossRefGoogle Scholar
[9]Fong, C. K. and Sourour, A. R., ‘On the operator identity ΣA kXBk = 0’, Canad. J. Math. 31 (1979), 845–857.CrossRefGoogle Scholar
[10]Gohberg, I. C. and Krein, M G., Introduction to the theory of linear nonselfadjoint operators, (Transl. Math. Monographs 18, Amer. Math. Soc., Providence, R. I., 1960).Google Scholar
[11]Harte, R., ‘Spectral mapping theorems,’ Proc. Roy. Irish Acad. Sect. A 72 (1972), 89–107.Google Scholar
[12]Harte, R., Invertibility and singularity for bounded linear operators, (Monographs and Textbooks in Pure and Applied Mathematics 109, Marcel Dekker, New York and Basel, 1988).Google Scholar
[13]Hladnik, M., ‘On prespeetrality of generalized derivations’, Proc. Roy. Soc. Edinburgh Sect. A 104 (1986), 93–106.Google Scholar
[14]Hladnik, M., When are generalized derivations spectral, Operator Theory: Advances and Appl. 24, pp. 215–226, Birkhäuser-Verlag, Basel, 1987).Google Scholar
[15]Mathieu, M., ‘Elementary operators on prime C*-algebras I’, Math. Ann. 284 (1989), 223–244.Google Scholar
[16]Ricker, W., ‘A commutativity criterion for prespectral operators’, Bull. Austral. Math. Soc. 36 (1987), 113–119.CrossRefGoogle Scholar


