Published online by Cambridge University Press: 09 April 2009
Let S = A0 hellip An be an n-simplex and Aih the foot of its altitude from its vertex Ai to its opposite prime face Si; O, G the circumcentre and centroid of S and Oi, Gi of Si. Representing the position vector of a point P, referred to O, by p, Coxeter [2] defines the Monge pointM of S Collinear with O and G by the relation 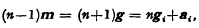 so that the Monge point Mi of Si is given by
so that the Monge point Mi of Si is given by 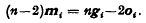 If the n+1 vectors a are related by
If the n+1 vectors a are related by 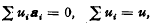 oi be given by
oi be given by 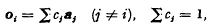 Aih is given by
Aih is given by 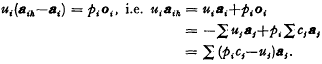 Since Aih lies in Si,
Since Aih lies in Si, 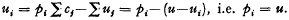 If Ti be a point on MiAih such that
If Ti be a point on MiAih such that 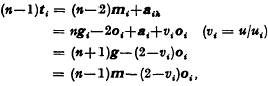 i.e.
i.e. 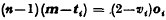 That is, MTi is parallel to ooi or normal to Si at Ti:. Or, the normals to the prime faces Si of S at their points Ti concur at M. In fact, this property of M has been used to prove by induction [3] that an S-point S of S lies at M. Thus M = 5, M = S or
That is, MTi is parallel to ooi or normal to Si at Ti:. Or, the normals to the prime faces Si of S at their points Ti concur at M. In fact, this property of M has been used to prove by induction [3] that an S-point S of S lies at M. Thus M = 5, M = S or 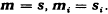 .
.