Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-26T18:40:11.288Z Has data issue: false hasContentIssue false
  • English
  • Français

Special series of unitary representations of groups acting on homogeneous trees

Part of: Locally compact groups and their algebras Structure and classification of infinite or finite groups

Published online by Cambridge University Press:  09 April 2009

Anna Maria Mantero  and
Anna Zappa
Anna Maria Mantero
Affiliation:
Istituto di Matematica, Via L. B. Alberti, 4 16132 Genova, Italy
Anna Zappa
Affiliation:
Istituto di Matematica, Via L. B. Alberti, 4 16132 Genova, Italy
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let G be a group acting faithfully on a homogeneous tree of order p + 1, p > 1. Let 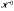be the space of functions on the Poission boundary ω, of zero mean on ω. When p is a prime. G is a discrete subgroup of PGL2(Qp) of finite covolume. The representations of the special series of PGL2(Qp), Which are irreducible and unitary in an appropriate completion of 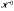, are shown to be reducible when restricted to G. It is proved that these representations of G are algebraically reducible on 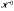and topologically irreducible on 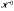endowed with the week topology.

MSC classification

Secondary: 22D10: Unitary representations of locally compact groups 20E05: Free nonabelian groups
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 40 , Issue 1 , February 1986 , pp. 83 - 88
Copyright
Copyright © Australian Mathematical Society 1986

References

[1]Betori, W. and Pagliacci, M., ‘Harmonic analysis for groups acting on trees’, Boll. Un. Mat. Ital. 63-B (1984), 333–349.Google Scholar
[2]Cecchini, C. and Figà-Talamanca, A., ‘Projections of uniqueness for Lp(G)’, Pacific J. Math. 51 (1974), 37–47.CrossRefGoogle Scholar
[3]Figà-Talamanca, A. and Picardello, M. A., ‘Spherical functions and harmonic analysis on free groups’, J. Fund. Anal. 47 (1982), 281–304.CrossRefGoogle Scholar
[4]Figà-Talamanca, A. and Picardello, M. A., Harmonic analysis on free groups (Lecture Notes in Pure and Applied Math., Vol. 87, Marcel Dekker, New York, 1983).Google Scholar
[5]Figà-Talamanca, A. and Picardello, M. A., ‘Restriction of spherical representations of PGL 2 (Qp) to a discrete subgroup’, Proc. Amer. Math. Soc. 91 (1984), 405–408.Google Scholar
[6]Ol'shanskii, G. I., ‘Classification of irreducible representations of groups of automorphisms of Bruhat-Tits trees’, Functional Anal. Appl. 11 (1977), 26–34.CrossRefGoogle Scholar
[7]Serre, J. P., ‘Arbres, amalgames, SL 2’, Astérisque 46 (1977).Google Scholar
[8]Silberger, A. J., PGL2 over the p-adics: its representations, spherical functions, and Fourier analysis (Lecture Notes in Math. 166, Springer-Verlag, Berlin, Heidelberg, New York, 1970).CrossRefGoogle Scholar