No CrossRef data available.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Published online by Cambridge University Press: 15 May 2013
Let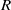 
$R$ be a commutative Noetherian ring, 
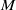$M$ be a finitely generated 
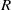$R$-module and 
$\mathfrak{a}$ be an ideal of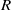 
$R$ such that 
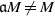$\mathfrak{a}M\not = M$. We show among the other things that, if 
$c$ is a nonnegative integer such that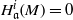 
${ H}_{\mathfrak{a}}^{i} (M)= 0$ for all 
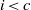$i\lt c$, then there is an isomorphism 
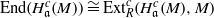$\mathrm{End} ({ H}_{\mathfrak{a}}^{c} (M))\cong { \mathrm{Ext} }_{R}^{c} ({ H}_{\mathfrak{a}}^{c} (M), M)$; and if 
$c$ is a nonnegative integer such that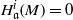 
${ H}_{\mathfrak{a}}^{i} (M)= 0$ for all 
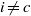$i\not = c$, there are the following isomorphisms:
(i)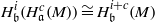 
$~\quad{ H}_{\mathfrak{b}}^{i} ({ H}_{\mathfrak{a}}^{c} (M))\cong { H}_{\mathfrak{b}}^{i+ c} (M)$ and
(ii)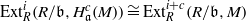 
$\quad{ \mathrm{Ext} }_{R}^{i} (R/ \mathfrak{b}, { H}_{\mathfrak{a}}^{c} (M))\cong { \mathrm{Ext} }_{R}^{i+ c} (R/ \mathfrak{b}, M)$
for all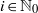 
$i\in { \mathbb{N} }_{0} $ and all ideals 
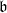$\mathfrak{b}$ of 
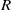$R$ with 
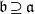$\mathfrak{b}\supseteq \mathfrak{a}$. We also prove that if 
$\mathfrak{a}$ and 
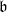$\mathfrak{b}$ are ideals of 
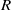$R$ with 
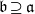$\mathfrak{b}\supseteq \mathfrak{a}$ and 
$c: = \mathrm{grade} (\mathfrak{a}, M)$, then there exists a natural homomorphism from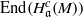 
$\mathrm{End} ({ H}_{\mathfrak{a}}^{c} (M))$ to 
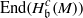$\mathrm{End} ({ H}_{\mathfrak{b}}^{c} (M))$, where 
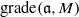$\mathrm{grade} (\mathfrak{a}, M)$ is the maximum length of 
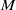$M$-sequences in 
$\mathfrak{a}$.
You have
Access