Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Olshen, Richard A.
1967.
Asymptotic properties of the periodogram of a discrete stationary process.
Journal of Applied Probability,
Vol. 4,
Issue. 3,
p.
508.
Nicholls, D. F.
1969.
TESTING FOR A JUMP IN CO‐SPECTRA1.
Australian Journal of Statistics,
Vol. 11,
Issue. 1,
p.
7.
1970.
Multiple Time Series.
p.
519.
Pagano, M.
1971.
Some asymptotic properties of a two-dimensional periodogram.
Journal of Applied Probability,
Vol. 8,
Issue. 4,
p.
841.
Walker, A. M.
1973.
On the estimation of a harmonic component in a time series with stationary dependent residuals.
Advances in Applied Probability,
Vol. 5,
Issue. 2,
p.
217.
Walker, A. M.
1973.
On the estimation of a harmonic component in a time series with stationary dependent residuals.
Advances in Applied Probability,
Vol. 5,
Issue. 2,
p.
217.
Davis, Herbert T.
1974.
Asymptotic properties of certain functionals of the periodogram.
Journal of Applied Probability,
Vol. 11,
Issue. 3,
p.
578.
Davis, Herbert T.
1974.
Asymptotic properties of certain functionals of the periodogram.
Journal of Applied Probability,
Vol. 11,
Issue. 03,
p.
578.
Swick, David A.
1975.
Asymptotic distribution of a discrete transform of an arbitrarily sampled homogeneous random field.
Advances in Applied Probability,
Vol. 7,
Issue. 1,
p.
140.
Swick, David A.
1975.
Asymptotic distribution of a discrete transform of an arbitrarily sampled homogeneous random field.
Advances in Applied Probability,
Vol. 7,
Issue. 1,
p.
140.
Wahba, G.
and
Wold, S.
1975.
Periodic splines for spectral density estimation: the use of cross validation for determining the degree of smoothing.
Communications in Statistics,
Vol. 4,
Issue. 2,
p.
125.
Wittwer, Gisela
1978.
Über die asymptotische verteilung des periodogramms stationärer gaussscher zufälliger folgen.
Series Statistics,
Vol. 9,
Issue. 3,
p.
357.
Rice, John
1979.
On the estimation of the parameters of a power spectrum.
Journal of Multivariate Analysis,
Vol. 9,
Issue. 3,
p.
378.
Zhao‐Guo, Chen
and
Hannan, E. J.
1980.
THE DISTRIBUTION OF PERIODOGRAM ORDINATES.
Journal of Time Series Analysis,
Vol. 1,
Issue. 1,
p.
73.
Heidelberger, Philip
and
Welch, Peter D.
1981.
A spectral method for confidence interval generation and run length control in simulations.
Communications of the ACM,
Vol. 24,
Issue. 4,
p.
233.
Wittwer, Gisela
1981.
Über die mehrdimensionalen asymptotischen verteilungen des periodogramms gaussscher stationärer folgen.
Series Statistics,
Vol. 12,
Issue. 3,
p.
361.
Engeman, Richard M.
Swanson, George D.
and
Jones, Richard H.
1983.
Optimal frequency locations for estimating model parameters in studies on respiratory control.
Computers and Biomedical Research,
Vol. 16,
Issue. 6,
p.
531.
Wittwer, Gisela
1983.
On the rate of convergence of the distribution of the periodogram matrix for gaussian vector processes.
Series Statistics,
Vol. 14,
Issue. 1,
p.
55.
Turkman, K. F.
and
Walker, A. M.
1984.
On the asymptotic distributions of maxima of trigonometric polynomials with random coefficients.
Advances in Applied Probability,
Vol. 16,
Issue. 4,
p.
819.
Turkman, K. F.
and
Walker, A. M.
1984.
On the asymptotic distributions of maxima of trigonometric polynomials with random coefficients.
Advances in Applied Probability,
Vol. 16,
Issue. 4,
p.
819.


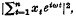 , plays an important part in methods of making inferences about the structure of {x
, plays an important part in methods of making inferences about the structure of {x