Article contents
Solution of a generalized Schroeder equation in two variables
Published online by Cambridge University Press: 09 April 2009
Extract
If f(z) is analytic at the origin, f(0)=0, and f′(0)=λ, where 0< λ <1, then Koenigs' [3] solution of Schroeder's equation w(f(z))=λw(z), with multiplier λ, is given by 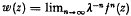 . Here fn(z) denotes the nth iterate of f(z), defined inductively as f0(z)=z, f(fn-1(z)), n=1, 2, 3, …. More generally the solution w(z) of Schroeder's equation is uniquely determined to within a multiplicative constant by the requirement that it be analytic at the origin. From the uniqueness it follows that if g(z) is analytic at the origin, vanishes there, and commutes with f(z), i.e., f(g(z)) = g(f(z)), then w(g(z)) = w(z), for some multiplier a. Since w′(0) = 1 for Koenig's' solution, it has an inverse locally, and we find that g(z) is uniquely determined by its linear part; in fact g(z) = w-1(μw(z)). In particular the integral iterates of f can be put in the form w-1(λw(z)) for integral n. Thus for any α, real or complex, we may define fα(z), consistent with the above definition when α is a positive integer, as w-1(λw(z)). In this manner any function g(z) of the above type can be considered as an iterate of /(z). Also if cc, j9, 0 are any two distinct points sufficiently close to the origin there exists an analytic function g(z) which commutes with f(z) such that g(0) = 0, g(α) = β. In fact g(z)=w-1(χw(z)), where the multiplier χ=w(β)(w(α))-1. These facts are all well known, e.g. [2] [5], and we shall establish analogous results in a more general situation.
. Here fn(z) denotes the nth iterate of f(z), defined inductively as f0(z)=z, f(fn-1(z)), n=1, 2, 3, …. More generally the solution w(z) of Schroeder's equation is uniquely determined to within a multiplicative constant by the requirement that it be analytic at the origin. From the uniqueness it follows that if g(z) is analytic at the origin, vanishes there, and commutes with f(z), i.e., f(g(z)) = g(f(z)), then w(g(z)) = w(z), for some multiplier a. Since w′(0) = 1 for Koenig's' solution, it has an inverse locally, and we find that g(z) is uniquely determined by its linear part; in fact g(z) = w-1(μw(z)). In particular the integral iterates of f can be put in the form w-1(λw(z)) for integral n. Thus for any α, real or complex, we may define fα(z), consistent with the above definition when α is a positive integer, as w-1(λw(z)). In this manner any function g(z) of the above type can be considered as an iterate of /(z). Also if cc, j9, 0 are any two distinct points sufficiently close to the origin there exists an analytic function g(z) which commutes with f(z) such that g(0) = 0, g(α) = β. In fact g(z)=w-1(χw(z)), where the multiplier χ=w(β)(w(α))-1. These facts are all well known, e.g. [2] [5], and we shall establish analogous results in a more general situation.
- Type
- Research Article
- Information
- Copyright
- Copyright © Australian Mathematical Society 1964
References
- 2
- Cited by


