Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-28T19:54:22.932Z Has data issue: false hasContentIssue false
  • English
  • Français

Soluble groups with complemented subnormal subgroups

To Bernhard Hermann Neumann on his 60th birthday

Published online by Cambridge University Press:  09 April 2009

R. Kochendörffer
R. Kochendörffer
Affiliation:
Department of Mathematics University of Tasmania Hobart, Tasmania
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A subgroup A of a group G is said to be complemented in G if G contains a subgroup C such that 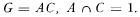. Every subgroup C with its property is called a complement of A in G. Various results have been obtained about groups in which each member of a given set of subgroups is complemented. Some of these results state, roughly speaking, that the existence of complements of all members of a given set of subgroups implies that all members of larger set are also complements. In this paper we derive another theorem of this kind.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 10 , Issue 3-4 , November 1969 , pp. 465 - 468
Copyright
Copyright © Australian Mathematical Society 1969

References

[1]Christensen, C., ‘Complementation in Groups’, Math. Z. 84 (1964), 52–69.CrossRefGoogle Scholar
[2]Hall, P., ‘Complemented Groups’, J. London Math. Soc. 12 (1937), 201–204.Google Scholar
[3]Baeva, N. V., ‘Completely Factorisable Groups’, Doklady Akad. Nauk S.S.S.R. (N.S.) 93 (1953), 877–880.Google Scholar
[4]Černikov, S. N., ‘Groups with Systems of Complemented Subgroups’ Mat. Sbornik 35 (77) (1954), 93–128.Google Scholar
[5]Dinerstein, N. T., ‘Finiteness Conditions in Groups with Systems of Complemented Subgroups’, Math. Z. 106 (1968), 321–326.Google Scholar
[6]Scott, W., Group Theory, Englewood Cliffs, New Jersey: Prentice Hall Inc. 1964.Google Scholar