Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-05T04:08:38.442Z Has data issue: false hasContentIssue false
  • English
  • Français

SOBOLEV SPACES ON LOCALLY COMPACT ABELIAN GROUPS AND THE BOSONIC STRING EQUATION

Part of: Abstract harmonic analysis Quantum field theory; related classical field theories Miscellaneous topics - Partial differential equations Linear function spaces and their duals

Published online by Cambridge University Press:  14 October 2014

PRZEMYSŁAW GÓRKA  and
ENRIQUE G. REYES
PRZEMYSŁAW GÓRKA
Affiliation:
Instituto de Matemática y Física, Universidad de Talca, Casilla 747, Talca, Chile Department of Mathematics and Information Sciences, Warsaw University of Technology, Pl. Politechniki 1, 00-661 Warsaw, Poland email [email protected]
ENRIQUE G. REYES*
Affiliation:
Departamento de Matemática y Ciencia de la Computación, Universidad de Santiago de Chile, Casilla 307 Correo 2, Santiago, Chile email [email protected], [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Motivated by a class of nonlinear nonlocal equations of interest for string theory, we introduce Sobolev spaces on arbitrary locally compact abelian groups and we examine some of their properties. Specifically, we focus on analogs of the Sobolev embedding and Rellich–Kondrachov compactness theorems. As an application, we prove the existence of continuous solutions to a generalized bosonic string equation posed on an arbitrary compact abelian group, and we also remark that our approach allows us to solve very general linear equations in a 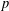$p$-adic context.

Keywords

abstract harmonic analysisSobolev spacesembedding theoremslocally compact groupsnonlinear nonlocal equationsstring theory

MSC classification

Primary: 43A15: $L^p$-spaces and other function spaces on groups, semigroups, etc.
Secondary: 46E35: Sobolev spaces and other spaces of “smooth” functions, embedding theorems, trace theorems 35S: Pseudodifferential operators and other generalizations of partial differential operators 81T30: String and superstring theories; other extended objects (e.g., branes)
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 98 , Issue 1 , February 2015 , pp. 39 - 53
Copyright
Copyright © 2014 Australian Mathematical Publishing Association Inc. 

References

Adams, R. A., Sobolev Spaces (Academic Press, New York, 1975).Google Scholar
Aref’eva, I. Ya. and Volovich, I. V., ‘Cosmological daemon’, J. High Energy Phys. 102(8) (2011), 32.Google Scholar
Bahouri, H., Fermanian-Kammerer, C. and Gallagher, I., ‘Analyse de l’espace des phases et calcul pseudo-differential sur le groupe de Heisenberg’, C. R. Math. Acad. Sci. Paris 347(17–18) (2009), 1021–1024.CrossRefGoogle Scholar
Barnaby, N., ‘A new formulation of the initial value problem for nonlocal theories’, Nuclear Phys. B 845 (2011), 1–29.Google Scholar
Barnaby, N., Biswas, T. and Cline, J. M., ‘p-adic inflation’, J. High Energy Phys. 0704 (2007), 056 35 pp.CrossRefGoogle Scholar
Berezansky, Y. M. and Kondratiev, Y. G., Spectral Methods in Infinite-Dimensional Analysis, Vols. 1–2 (Kluwer, Dordrecht, 1995).CrossRefGoogle Scholar
Brekke, L. and Freund, P. G. O., ‘p-adic numbers in physics’, Phys. Rep. 233 (1993), 1–66.CrossRefGoogle Scholar
Calcagni, G., Montobbio, M. and Nardelli, G., ‘Route to nonlocal cosmology’, Phys. Rev. D 76 (2007), 126001, 20 pp.Google Scholar
Calcagni, G., Montobbio, M. and Nardelli, G., ‘Localization of nonlocal theories’, Phys. Lett. B 662 (2008), 285–289.Google Scholar
Deitmer, A. and Echterhoff, S., Principles of Harmonic Analysis (Springer, New York, 2009).Google Scholar
Eliezer, D. A. and Woodard, R. P., ‘The problem of nonlocality in string theory’, Nuclear Phys. B 325 (1989), 389–469.Google Scholar
Feichtinger, H. G., ‘Compactness in translation invariant Banach spaces of distributions and compact multipliers’, J. Math. Anal. Appl. 102 (1984), 289–327.CrossRefGoogle Scholar
Feichtinger, H. G. and Gürkanli, A. T., ‘On a family of weighted convolution algebras’, Int. J. Math. Math. Sci. 13 (1990), 517–526.Google Scholar
Feichtinger, H. G., Pandey, S. S. and Werther, T., ‘Minimal norm interpolation in harmonic Hilbert spaces and Wiener amalgam spaces on locally compact abelian groups’, J. Math. Kyoto Univ. 47(1) (2007), 65–78.Google Scholar
Feichtinger, H. G. and Werther, T., ‘Robustness of regular sampling in Sobolev algebras’, in: Sampling, Wavelets and Tomography (eds. Benedetto, J. and Zayed, A. I.) (Birkhäuser, Boston, MA, 2004), 83–113.CrossRefGoogle Scholar
Górka, P., ‘Pego theorem on locally compact abelian groups’, J. Algebra Appl. 13 1350143 (2014).CrossRefGoogle Scholar
Górka, P., Prado, H. and Reyes, E. G., ‘Nonlinear equations with infinitely many derivatives’, Complex Anal. Oper. Theory 5 (2011), 313–323.Google Scholar
Górka, P., Prado, H. and Reyes, E. G., ‘Generalized euclidean bosonic string equations’, in: Operator Theory: Advances and Applications, Vol. 224 (Springer, Basel, 2012), 147–169.Google Scholar
Górka, P., Prado, H. and Reyes, E. G., ‘On a general class of nonlocal equations’, Ann. Henri Poincaré 14 (2013), 947–966.Google Scholar
Górka, P. and Reyes, E. G., ‘The modified Camassa–Holm equation’, Int. Math. Res. Not. IMRN 2011(12) (2011), 2617–2649.Google Scholar
Gröchenig, K. and Strohmer, T., ‘Pseudodifferential operators on locally compact abelian groups and Sjöstrand’s symbol class’, J. reine angew. Math. 613 (2007), 121–146.Google Scholar
Hajłasz, P., ‘Sobolev spaces on an arbitrary metric space’, Potential Anal. 5(4) (1996), 403–415.Google Scholar
Hajłasz, P. and Koskela, P., ‘Sobolev met Poincaré’, Mem. Amer. Math. Soc. 145(688) (2000).Google Scholar
Hebey, E., Sobolev Spaces on Riemannian Manifolds, Lecture Notes in Mathematics, 1635 (Springer, Berlin, 1996).CrossRefGoogle Scholar
Hewitt, E. and Ross, K. A., Abstract Harmonic Analysis, Vol. I: Structure of Topological Groups. Integration Theory. Group Representations; Vol. II: Structure and Analysis for Compact Groups. Analysis on Locally Compact Abelian Groups (Springer, New York–Berlin, 1963, 1970).Google Scholar
Kolmogorov, A. N., ‘Über Kompaktheit der Funktionenmengen bei der Konvergenz im Mittel’, Nachr. Ges. Wiss. Göttingen 9 (1931), 60–63.Google Scholar
Kostelecký, V. A. and Samuel, S., ‘On a nonperturbative vacuum for the open bosonic string’, Nuclear Phys. B 336 (1990), 263–296.Google Scholar
Moeller, N. and Zwiebach, B., ‘Dynamics with infinitely many time derivatives and rolling tachyons’, J. High Energy Phys. 34(10) (2002), 38.Google Scholar
Moffat, J. W., ‘Ultraviolet complete electroweak model without a Higgs particle’, Eur. Phys. J. Plus 126 (2011), 53.Google Scholar
Rodríguez-Vega, J. J. and Zúñiga-Galindo, W. A., ‘Elliptic pseudodifferential equations and Sobolev spaces over p-adic fields’, Pacific J. Math. 246(2) (2010), 407–420.Google Scholar
Ruzhansky, M. and Turunen, V., Pseudo-Differential Operators and Symmetries. Background Analysis and Advanced Topics (Birkhäuser, Basel–Boston–Berlin, 2010).Google Scholar
Shanmugalingam, N., ‘Newtonian spaces: an extension of Sobolev spaces to metric measure spaces’, Rev. Mat. Iberoam. 16(2) (2000), 243–279.Google Scholar
Stroock, D. W., ‘Logarithmic Sobolev inequalities for Gibbs states’, in: Corso CIME (Springer, Berlin–Heidelberg, 1993).Google Scholar
Tateoka, J., ‘On the characterization of Hardy–Besov spaces on the dyadic group and its applications’, Studia Math. 110 (1994), 127–148.Google Scholar
Tausk, D. V., ‘A locally compact non divisible abelian group whose character group is torsion free and divisible’, Canad. Math. Bull. 56 (2013), 213–217.Google Scholar
Taylor, M. E., Partial Differential Equations, Vol. I (Springer, New York, 1996).Google Scholar
Vishik, M. I. and Fursikov, A. V., Mathematical Problems of Statistical Hydromechanics (Kluwer Academic, Dordrecht–Boston–London, 1980).Google Scholar
Vladimirov, V. S., ‘The equation of the p-adic open string for the scalar tachyon field’, Izv. Math. 69 (2005), 487–512.Google Scholar
Vladimirov, V. S. and Volovich, Ya. I., ‘Nonlinear dynamics equation in p-adic string theory’, Teoret. Mat. Fiz. 138 (2004), 355–368; translation in Theoret. Math. Phys. 138 (2004), 297–309.Google Scholar
Weil, A., L’intégration dans les groupes topologiques et ses applications (Hermann, Paris, 1940).Google Scholar
Witten, E., ‘Noncommutative geometry and string field theory’, Nucl. Phys. B 268 (1986), 253–294.Google Scholar