No CrossRef data available.
Published online by Cambridge University Press: 26 April 2021
Let 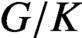 $G/K$
be an irreducible symmetric space, where G is a noncompact, connected Lie group and K is a compact, connected subgroup. We use decay properties of the spherical functions to show that the convolution product of any
$G/K$
be an irreducible symmetric space, where G is a noncompact, connected Lie group and K is a compact, connected subgroup. We use decay properties of the spherical functions to show that the convolution product of any 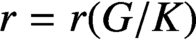 $r=r(G/K)$
continuous orbital measures has its density function in
$r=r(G/K)$
continuous orbital measures has its density function in 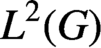 $L^{2}(G)$
and hence is an absolutely continuous measure with respect to the Haar measure. The number r is approximately the rank of
$L^{2}(G)$
and hence is an absolutely continuous measure with respect to the Haar measure. The number r is approximately the rank of 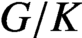 $G/K$
. For the special case of the orbital measures,
$G/K$
. For the special case of the orbital measures, 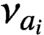 $\nu _{a_{i}}$
, supported on the double cosets
$\nu _{a_{i}}$
, supported on the double cosets 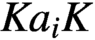 $Ka_{i}K$
, where
$Ka_{i}K$
, where 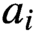 $a_{i}$
belongs to the dense set of regular elements, we prove the sharp result that
$a_{i}$
belongs to the dense set of regular elements, we prove the sharp result that 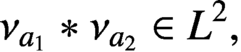 $\nu _{a_{1}}\ast \nu _{a_{2}}\in L^{2},$
except for the symmetric space of Cartan class
$\nu _{a_{1}}\ast \nu _{a_{2}}\in L^{2},$
except for the symmetric space of Cartan class 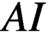 $AI$
when the convolution of three orbital measures is needed (even though
$AI$
when the convolution of three orbital measures is needed (even though  $\nu _{a_{1}}\ast \nu _{a_{2}}$
is absolutely continuous).
$\nu _{a_{1}}\ast \nu _{a_{2}}$
is absolutely continuous).
Communicated by Robert Yuncken
This research is supported in part by NSERC 2016-03719 and by Sultan Qaboos University. The authors thank Acadia University for their hospitality when this research was done.